바다에 퐁당 Ꙭ̮ ꉂ ◡̈⋆*

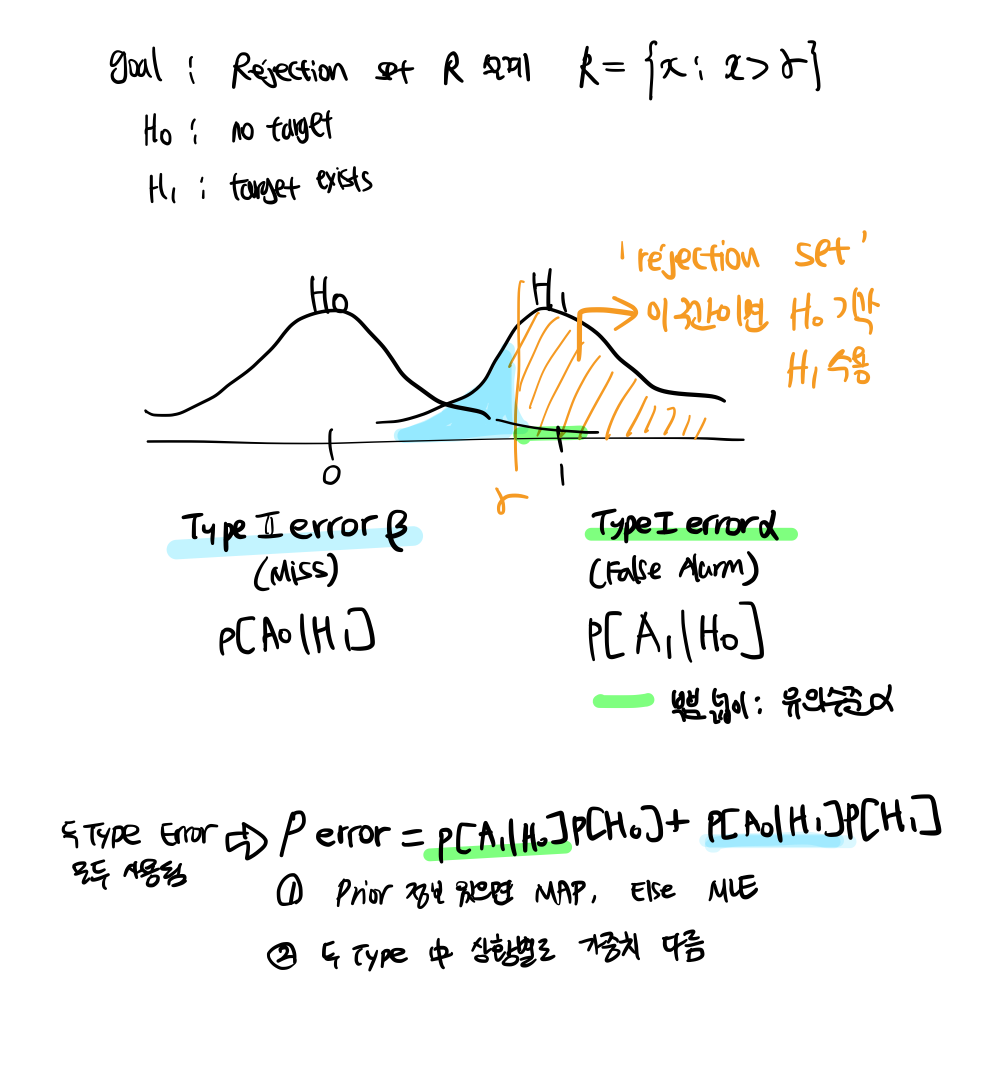
Bid Price와 Ask Price는 매수자와 매도자의 거래 의사를 나타냄

Market Maker는 이 두 가격을 제시하고 거래를 중개하여 유동성을 제공함

투자자 A는 Ask Price에 채권을 매수하고, 투자자 B는 Bid Price에 채권을 매도하여 거래가 성사됨 

Market Maker는 Bid와 Ask의 차이인 스프레드를 통해 수익을 얻음

기본 설정

• 채권: 만기 10년, 액면가 $1,000, 쿠폰 금리 5% (즉, 매년 $50 지급)
• 시장 상황:
  • Bid Price: $980
  • Ask Price: $990
  • 스프레드: $10 ($990 - $980)

시나리오 단계별 설명

1. 시장 참가자들
   • 투자자 A: 채권을 사고 싶어합니다.
   • 투자자 B: 채권을 팔고 싶어합니다.
   • Market Maker M: 채권의 유동성을 제공하며 거래를 중개합니다.
2. Bid Price와 Ask Price 제시
   • Market Maker M은 채권의 Bid Price를 $980, Ask Price를 $990로 제시합니다.
   • 이 의미는 M이 $980에 채권을 매수할 준비가 되어 있고, $990에 채권을 매도할 준비가 되어 있다는 것입니다.
3. 투자자 A의 행동
   • 투자자 A는 이 채권을 매수하고 싶어합니다. 시장에서 가장 저렴한 매도 가격인 Ask Price $990에 매수 주문을 냅니다.
   • 이로 인해 A는 채권을 $990에 매수합니다.
4. 투자자 B의 행동
   • 투자자 B는 이 채권을 매도하고 싶어합니다. 시장에서 가장 높은 매수 가격인 Bid Price $980에 매도 주문을 냅니다.
   • 이로 인해 B는 채권을 $980에 매도합니다.
5. Market Maker의 역할
   • Market Maker M은 $980에 채권을 매수하고, $990에 채권을 매도했습니다.
   • M의 수익은 스프레드인 $10입니다.

추가적인 시나리오 요소

1. 변동성 요소
   • 시장 상황에 따라 Bid Price와 Ask Price는 변동할 수 있습니다.
   • 예를 들어, 경제 지표 발표, 금리 변화, 채권 발행자의 신용도 변화 등으로 인해 가격이 변동할 수 있습니다.
2. 대량 주문의 영향
   • 만약 투자자 A가 대량의 채권을 매수하려 한다면, 이는 시장 가격에 영향을 줄 수 있습니다.
   • Market Maker M은 충분한 채권을 보유하고 있지 않다면 추가적인 채권을 확보하기 위해 가격을 조정할 수 있습니다.

*위 글은 chat gpt를 활용, 필자가 퇴고하여 작성된 글입니다.

이표채의 쿠폰 금리(coupon rate)와 만기 수익률(Yield to Maturity, YTM)의 관계

요약
   - 이표채 발행 당시: 쿠폰 금리 = YTM
   -시장 금리 상승 후: 쿠폰 금리 < YTM
   -시장 금리 하락 후: 쿠폰 금리 > YTM

0. 발행 당시 채권 쿠폰 금리와 YTM이 같다?

- 모든 이표채는 '액면가로 발행'됨: 즉 채권 발행 당시 채권의 가격은 == 채권의 액면가(만기에 상환하는 금액)과 동일함

(zeros. 즉 순할인채는 말 그대로 할인된 가격으로..)

- YTM은 채권 가격이 결정된 후에야 사후적으로 계산되는 수익률 값임. 즉, 전적으로 채권 가격에 의존함.

- 채권 발행 당시, 채권 fair pricing 방법 자체가

   => 채권의 고정된 CF, 즉 쿠폰+원금 포함하는 현금흐름 각각에 대해 PV시켜서 summation시킨 값을 채권 가격으로 결정함

   => 이때 액면가와 채권가격이 일치하므로 이표채 발행 당시의 YTM == coupon rate가 됨.

1. 쿠폰 금리 (Coupon Rate):
   - 쿠폰 금리는 채권 발행 시 정해진 이자율로, 채권 발행자가 정기적으로 채권 보유자에게 지급하는 이자의 비율을 말합니다. 예를 들어, 1000달러짜리 채권의 쿠폰 금리가 5%라면, 채권 보유자는 매년 50달러의 이자를 받게 됩니다.

2. 만기 수익률 (Yield to Maturity, YTM):
   - 만기 수익률은 채권을 만기까지 보유할 경우 얻을 수 있는 총 수익률을 나타내며, 이자 지급과 원금 상환을 모두 포함한 수익률입니다. 이는 시장 이자율, 채권 가격, 남은 기간 등 여러 요인을 고려하여 계산됩니다.

3. 발행 당시의 관계:
   - 채권 발행 시: 채권이 발행될 때, 쿠폰 금리와 YTM은 동일합니다. 이는 발행 당시 채권의 시장 가격이 액면가(face value)와 같기 때문입니다.
     - 예를 들어, 액면가가 1000달러이고 쿠폰 금리가 5%인 채권이 1000달러에 발행되면, 이 채권의 YTM도 5%가 됩니다.

4. 발행 이후의 관계 변화:
   - 시장 금리 상승: 만약 시장 금리가 상승하면, 기존 채권의 YTM은 쿠폰 금리보다 높아집니다. 이는 기존 채권의 가격이 떨어지기 때문입니다. 투자자들은 더 높은 시장 금리를 얻기 위해 기존 채권의 가격을 할인하여 구매하게 됩니다.
     - 예를 들어, 시장 금리가 6%로 상승하면, 기존의 5% 쿠폰 금리를 가진 채권은 가격이 떨어져야 YTM이 6%에 맞춰집니다.
   
   - 시장 금리 하락: 반대로, 시장 금리가 하락하면 기존 채권의 YTM은 쿠폰 금리보다 낮아집니다. 이는 기존 채권의 가격이 상승하기 때문입니다. 더 높은 쿠폰 금리를 제공하는 채권은 더 높은 가격에 거래됩니다.
     - 예를 들어, 시장 금리가 4%로 하락하면, 기존의 5% 쿠폰 금리를 가진 채권은 가격이 올라가야 YTM이 4%에 맞춰집니다.

*위 글은 chat gpt의 자료제공 + 필자의 퇴고를 거쳐 작성되었습니다

가설검증 Hypothesis Testing

가설검증(Hypothesis Testing): 주어진 데이터가 어떤 가설을 지지하는지 또는 반박하는지를 판단하는 과정
 
**

통계학에서 **검정**과 **검증**은 비슷해 보이지만 다른 의미를 가지고 있습니다.

1. **검정 (Hypothesis Testing)**:
   - 검정은 특정 가설이 통계적으로 유의미한지 여부를 판단하는 과정입니다. 
   - 예를 들어, 두 집단의 평균이 동일한지 검정하는 t-검정이나, 분산이 같은지 검정하는 F-검정 등이 있습니다.
   - 검정의 결과로 귀무가설(보통 "차이가 없다"는 가설)을 기각할지 여부를 결정합니다. 검정의 핵심은 데이터로부터 얻은 증거가 가설을 지지할 만큼 충분한지 평가하는 것입니다.

2. **검증 (Verification)**:
   - 검증은 어떤 모델이나 시스템, 방법론이 제대로 작동하는지 확인하는 과정입니다.
   - 이는 실험이나 관찰을 통해 주어진 조건 하에서 이론적 주장이나 방법이 실제로 일치하는지를 점검하는 것입니다.
   - 예를 들어, 통계 모델을 만들었을 때, 그 모델이 실제 데이터를 잘 설명하는지를 검증합니다.

정리하자면, **검정**은 주어진 가설이 데이터에 의해 지지되는지를 평가하는 과정이고, **검증**은 이론이나 모델이 제대로 작동하는지를 확인하는 과정입니다.

두 가지 가설을 세우고, 

• 귀무가설(Null Hypothesis, 𝐻0): 일반적으로 기존의 믿음이나 가정, 또는 차이가 없음을 주장하는 가설임.
• 대립가설(Alternative Hypothesis, 𝐻1): 귀무가설과 반대되는 주장으로, 차이나 효과가 있음을 주장하는 가설임.

통계적 방법을 통해 이들 가설을 검증하는 방식

가설검증=검정의 단계

가설검증은 다음과 같은 단계로 이루어짐

1. 가설 설정:
   • 귀무가설 (𝐻0​): 데이터에 차이가 없다고 주장함
   • 대립가설 (𝐻1): 데이터에 차이가 있다고 주장함
2. 유의수준 설정 (𝛼):
   • 일반적으로 0.05나 0.01 같은 값
   • 귀무가설이 참일 때, 잘못 기각할 확률 (False Positive이 확률)
3. 검정 통계량 계산:
   • 데이터를 기반으로 검정 통계량을 계산함.
   • 이 통계량은 보통 표준정규분포(Z-검정), t-분포(t-검정) 등 여러 가지 방법이 있음.
4. p-값 계산:
   • 검정 통계량이 주어진 분포에서 어느 정도의 극단적인 값을 갖는지를 계산함.
   • p-값: 귀무가설(영가설)이 참일 때, 검정 통계량이 현재 관측된 값보다 극단적인 값을 가질 확률임.
5. 결정:
   • p-값을 유의수준 (𝛼)와 비교
   • if p값 <  𝛼, 귀무가설을 기각하고 대립가설을 채택 (실험 결과 P값이 작아야 실험 가정이 유의하다)
   • p-값이 𝛼보다 크면, 귀무가설을 기각하지 않음

예시

예제: 평균 비교

두 집단의 평균이 같은지 비교 -> 신약이 기존 약보다 효과가 있는지를 검증한다고 가정

1. 가설 설정:
   • 𝐻0​: 두 집단의 평균이 같음 (𝜇1=𝜇2​)
   • 𝐻1​: 두 집단의 평균이 다름 (𝜇1≠𝜇2​)
2. 유의수준 설정:
   • 𝛼=0.05
3. 검정 통계량 계산:
   • t-검정을 사용해 두 집단의 평균 차이를 검정
4. p-값 계산:
   • 계산된 t-값에 대응하는 p-값을 찾음
5. 결정:
   • p-값이 0.05보다 작으면, 귀무가설을 기각하고 신약이 기존 약과 효과가 다르다고 결론지음.

유형별 가설검증

가설검증에는 여러 유형이 있음:

• Z-검정: 표본 크기가 크고, 모분산이 알려진 경우
• t-검정: 표본 크기가 작고, 모분산이 알려지지 않은 경우
• 카이제곱검정: 범주형 데이터의 독립성이나 적합성 검정에 사용
• F-검정: 두 집단의 분산 비교에 사용

가설검증의 오류

가설검증에서는 두 가지 주요 오류가 발생할 수 있음:

• 제1종 오류 (Type I Error): 귀무가설이 참인데 기각하는 오류 (유의수준 𝛼)
  • False Positive
  • 예시: 암 진단 검사에서 실제로 암이 없는데도 검사가 암이 있다고 잘못 진단하는 경우
  • 유의수준 (𝛼): 제1종 오류가 발생할 확률. 연구자가 설정하는 값으로, 보통 0.05 (5%)나 0.01 (1%) 같은 값을 사용
    • 의미: α=0.05라면, 귀무가설이 참일 때 5%의 확률로 귀무가설을 잘못 기각할 수 있다
• 제2종 오류 (Type II Error): 귀무가설이 거짓인데 기각하지 않는 오류 (베타 𝛽)
  • False Negative
  • 예시: 암 진단 검사에서 실제로 암이 있는데도 검사가 암이 없다고 잘못 진단하는 경우
  • 베타 (𝛽): 제2종 오류가 발생할 확률. 유의수준과 달리 보통 명시적으로 설정되지 않고 계산을 통해 결정
    • 검정력 (Power): 1 - 𝛽를 검정력이라고 함. 실제로 대립가설이 참일 때 이를 올바르게 기각할 확률
    • 검정력이 높을수록 좋은 검사.

제1종 오류와 제2종 오류 Trade-off

𝛼를 낮추면 제1종 오류의 확률은 줄어들지만, 𝛽는 증가해서 제2종 오류의 확률이 커질 수 있음
vice versa

오류 조절 방법

• 유의수준 (𝛼) 조정: 보통 연구자는 𝛼α를 0.05나 0.01로 설정하지만, 문제의 심각성에 따라 더 낮추거나 높일 수 있음.
• 표본 크기 증가: 표본 크기를 늘리면 검정력이 높아져서 제2종 오류의 확률을 줄일 수 있음. 이는 더 많은 데이터를 수집함으로써 오류를 줄이는 방법임.
• 효과 크기 증가: 효과 크기가 클수록 검정력이 높아져서 제2종 오류의 확률이 줄어듦. 연구 설계를 통해 더 뚜렷한 차이를 만들 수 있는 방법을 고려할 수 있음.

* P_err = Total probablility of error of a binary hypothesis test
 
 
 
*일부 gpt를 활용하여 작성함

Bias 은 예측값과 정답의 차이 정도, Variance 은 예측값끼리의 차이 정도
과소적합(Underfitting): High bias
과적합(Overfitting): High variance
 
MSE = Bias + Variance
Bias-Variance Tradeoff!

https://towardsdatascience.com/understanding-the-bias-variance-tradeoff-165e6942b229?gi=3507c8a8e592

https://velog.io/@iguv/Bias-and-Variance#:~:text=Bias%20%EC%9D%80%20%EC%98%88%EC%B8%A1%EA%B0%92%EA%B3%BC%20%EC%A0%95%EB%8B%B5%EC%9D%98%20%EC%B0%A8%EC%9D%B4%20%EC%A0%95%EB%8F%84%2C%20Variance%20%EC%9D%80,%ED%95%A9%EC%9D%80%20High%20variance%20%EC%9D%B4%EB%8B%A4.
https://modulabs-biomedical.github.io/Bias_vs_Variance

1. MGF(Moment Generating Function)

Q. Binomial Distribution의 MGF가 무엇인가?

Q1. MGF가 뭔데

Moment: 랜덤변수의 분포를 나타내는 주요 정보 .. E[X^n]으로 표현

1차 Moment = E[X^1] → 평균

2차 Moment = E[X^2] → 1차와 조합하여 분산 표현

3차 Moment = E[X^3] ...

Moment 정보들이 더 많을수록 랜덤변수를 구체적으로 이해할 수 있게 됨

그러면 분포마다 Moment가 있다는 건데.

Moment는 어떻게 알 수 있을까?

Moment를 생성하는 함수가 따로 있음. 그게 MGF임! ㅎㅎ

어떤 RV X에 대하여

가 정의되는 t가 존재하는 경우 

Mx(t) = X의 moment generating function (실제 입력변수는 t, 어차피 t=0만 입력하긴 함)

을 통해 Mx(t)가 정의된다.

단순히 E[e^(tX)]를 적분 형태로 풀어쓴 후 양변 미분해버리면 저런 꼴이 나옴

랜덤변수 X에 대해, t=0 입력할 때 n번째의 moment가 생성되는 구조,,

Q2. MGF에 대한 추가 성질

(1)

proof

(2)

(3)

서로 독립적인 포아송분포의 RV / 가우시안분포 RV

들의 합으로 이루어진 새로운 RV

-> 마찬가지로 포아송분포 / 가우시안분포를 따름

그 proof를 MGF를 가지고 해버리네

여러 RVs가 exponential 분포 따르면서 + iid관계이면 => 그 RVs의 합은 어랑분포를 따름

- 새로운 MGF가 나타났을 때 각 moment들을 계산할 줄 알아야 하고

- 새로운 분포에 대해 그것의 MGF를 구할 줄 알아야 함

Q. Binomial Distribution의 MGF가 무엇인가?

2. Binomial Theorem

진짜로 그러하다

3. Central Limit Theorem은 다음 기회에 ..😊

https://elementary-physics.tistory.com/135