728x90
가설검증 Hypothesis Testing
가설검증(Hypothesis Testing): 주어진 데이터가 어떤 가설을 지지하는지 또는 반박하는지를 판단하는 과정
**
통계학에서 **검정**과 **검증**은 비슷해 보이지만 다른 의미를 가지고 있습니다.
1. **검정 (Hypothesis Testing)**:
- 검정은 특정 가설이 통계적으로 유의미한지 여부를 판단하는 과정입니다.
- 예를 들어, 두 집단의 평균이 동일한지 검정하는 t-검정이나, 분산이 같은지 검정하는 F-검정 등이 있습니다.
- 검정의 결과로 귀무가설(보통 "차이가 없다"는 가설)을 기각할지 여부를 결정합니다. 검정의 핵심은 데이터로부터 얻은 증거가 가설을 지지할 만큼 충분한지 평가하는 것입니다.
2. **검증 (Verification)**:
- 검증은 어떤 모델이나 시스템, 방법론이 제대로 작동하는지 확인하는 과정입니다.
- 이는 실험이나 관찰을 통해 주어진 조건 하에서 이론적 주장이나 방법이 실제로 일치하는지를 점검하는 것입니다.
- 예를 들어, 통계 모델을 만들었을 때, 그 모델이 실제 데이터를 잘 설명하는지를 검증합니다.
정리하자면, **검정**은 주어진 가설이 데이터에 의해 지지되는지를 평가하는 과정이고, **검증**은 이론이나 모델이 제대로 작동하는지를 확인하는 과정입니다.
두 가지 가설을 세우고,
- 귀무가설(Null Hypothesis, 𝐻0): 일반적으로 기존의 믿음이나 가정, 또는 차이가 없음을 주장하는 가설임.
- 대립가설(Alternative Hypothesis, 𝐻1): 귀무가설과 반대되는 주장으로, 차이나 효과가 있음을 주장하는 가설임.
통계적 방법을 통해 이들 가설을 검증하는 방식
가설검증=검정의 단계
가설검증은 다음과 같은 단계로 이루어짐
- 가설 설정:
- 귀무가설 (𝐻0): 데이터에 차이가 없다고 주장함
- 대립가설 (𝐻1): 데이터에 차이가 있다고 주장함
- 유의수준 설정 (𝛼):
- 일반적으로 0.05나 0.01 같은 값
- 귀무가설이 참일 때, 잘못 기각할 확률 (False Positive이 확률)
- 검정 통계량 계산:
- 데이터를 기반으로 검정 통계량을 계산함.
- 이 통계량은 보통 표준정규분포(Z-검정), t-분포(t-검정) 등 여러 가지 방법이 있음.
- p-값 계산:
- 검정 통계량이 주어진 분포에서 어느 정도의 극단적인 값을 갖는지를 계산함.
- p-값: 귀무가설(영가설)이 참일 때, 검정 통계량이 현재 관측된 값보다 극단적인 값을 가질 확률임.
- 결정:
- p-값을 유의수준 (𝛼)와 비교
- if p값 < 𝛼, 귀무가설을 기각하고 대립가설을 채택 (실험 결과 P값이 작아야 실험 가정이 유의하다)
- p-값이 𝛼보다 크면, 귀무가설을 기각하지 않음
예시
예제: 평균 비교
두 집단의 평균이 같은지 비교 -> 신약이 기존 약보다 효과가 있는지를 검증한다고 가정
- 가설 설정:
- 𝐻0: 두 집단의 평균이 같음 (𝜇1=𝜇2)
- 𝐻1: 두 집단의 평균이 다름 (𝜇1≠𝜇2)
- 유의수준 설정:
- 𝛼=0.05
- 검정 통계량 계산:
- t-검정을 사용해 두 집단의 평균 차이를 검정
- p-값 계산:
- 계산된 t-값에 대응하는 p-값을 찾음
- 결정:
- p-값이 0.05보다 작으면, 귀무가설을 기각하고 신약이 기존 약과 효과가 다르다고 결론지음.
유형별 가설검증
가설검증에는 여러 유형이 있음:
- Z-검정: 표본 크기가 크고, 모분산이 알려진 경우
- t-검정: 표본 크기가 작고, 모분산이 알려지지 않은 경우
- 카이제곱검정: 범주형 데이터의 독립성이나 적합성 검정에 사용
- F-검정: 두 집단의 분산 비교에 사용
가설검증의 오류
가설검증에서는 두 가지 주요 오류가 발생할 수 있음:
- 제1종 오류 (Type I Error): 귀무가설이 참인데 기각하는 오류 (유의수준 𝛼)
- False Positive
- 예시: 암 진단 검사에서 실제로 암이 없는데도 검사가 암이 있다고 잘못 진단하는 경우
- 유의수준 (𝛼): 제1종 오류가 발생할 확률. 연구자가 설정하는 값으로, 보통 0.05 (5%)나 0.01 (1%) 같은 값을 사용
- 의미: 라면, 귀무가설이 참일 때 5%의 확률로 귀무가설을 잘못 기각할 수 있다
- 제2종 오류 (Type II Error): 귀무가설이 거짓인데 기각하지 않는 오류 (베타 𝛽)
- False Negative
- 예시: 암 진단 검사에서 실제로 암이 있는데도 검사가 암이 없다고 잘못 진단하는 경우
- 베타 (𝛽): 제2종 오류가 발생할 확률. 유의수준과 달리 보통 명시적으로 설정되지 않고 계산을 통해 결정
- 검정력 (Power): 1 - 𝛽를 검정력이라고 함. 실제로 대립가설이 참일 때 이를 올바르게 기각할 확률
- 검정력이 높을수록 좋은 검사.
제1종 오류와 제2종 오류 Trade-off
𝛼를 낮추면 제1종 오류의 확률은 줄어들지만, 𝛽는 증가해서 제2종 오류의 확률이 커질 수 있음
vice versa
오류 조절 방법
- 유의수준 (𝛼) 조정: 보통 연구자는 𝛼α를 0.05나 0.01로 설정하지만, 문제의 심각성에 따라 더 낮추거나 높일 수 있음.
- 표본 크기 증가: 표본 크기를 늘리면 검정력이 높아져서 제2종 오류의 확률을 줄일 수 있음. 이는 더 많은 데이터를 수집함으로써 오류를 줄이는 방법임.
- 효과 크기 증가: 효과 크기가 클수록 검정력이 높아져서 제2종 오류의 확률이 줄어듦. 연구 설계를 통해 더 뚜렷한 차이를 만들 수 있는 방법을 고려할 수 있음.
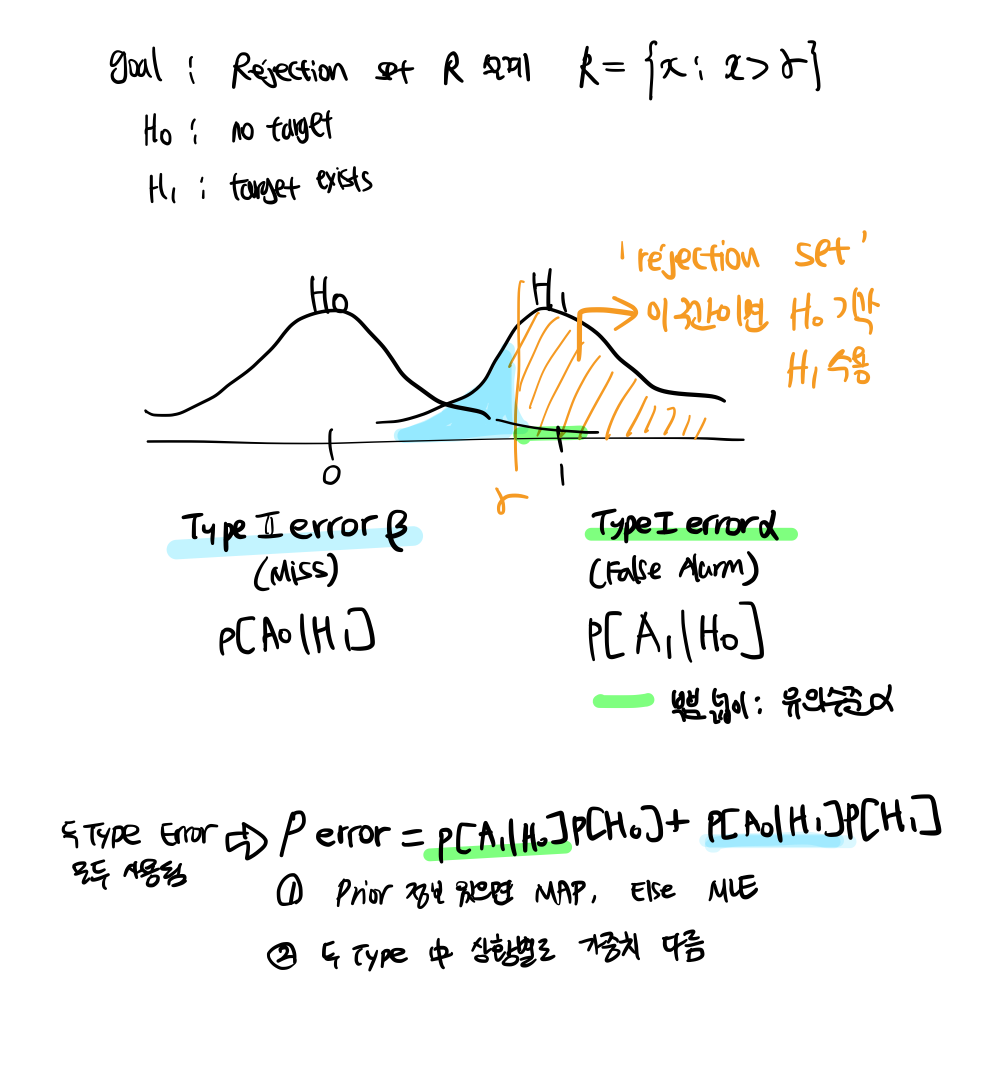
* P_err = Total probablility of error of a binary hypothesis test
*일부 gpt를 활용하여 작성함
728x90
'AI > Data Science' 카테고리의 다른 글
| LLM 프롬프트 엔지니어링, CoT (0) | 2024.07.10 |
|---|---|
| hugging face / Qwen2 snippent code (0) | 2024.06.17 |
| [Statistics] Bias vs Variance (1) | 2024.05.28 |
| [Statistics] MGF(Moment Generating Function), Binomial Theorem (1) | 2024.05.23 |
| [Statistics] 극좌표계, 직교좌표계, 야코비 행렬 등 응용하는 적분문제,, (0) | 2024.04.29 |