옵션
1. 미리 정해진 조건에 따라 일정한 기간 내에 상품이나 유가증권 등의 특정자산을 사거나 팔 수 있는 권리
2. 옵션의 두 타입: 콜옵션, 풋옵션
: 파생금융상품 중 하나로, 기초자산의 가격이 특정 수준에 도달할 때 이를 사고팔 수 있는 권리를 매매하는 계약
- 콜옵션은 만기일에 미리 정해진 가격(행사가격)으로 기초자산을 매수할 수 있는 권리 (사기)
- 풋옵션은 만기일에 미리 정해진 가격(행사가격)으로 기초자산을 매도할 수 있는 권리 (팔기)
→ 기초자산의 미래상황에 따라 옵션 거래에 따른 수익이 좌우됨
→ 옵션 가치 평가: '수익의 크기 x 확률'
→ 기초자산의 움직임(ex. 주식의 움직임)을 확률분포로 표시할 수 있다면 옵션가격을 합리적으로 계산할 수 있음
3. 고려할 특성
1) 기초자산의 미래가격: 현재가격을 기점으로 증가 범위 & 감소 범위가 대략 비슷함 (=기초자산의 미래 가격 분포가 좌우대칭)
2) 가격변동은 연속적임
3) 기초자산의 가격이 음수가 될 수 없음 (1,2에 따라 정규분포가 될 수 없는 이유)
→ 기초자산가격 자체가 아닌, '기초자산가격의 변화율/수익률이 정규분포를 따른다'고 가정
→ 옵션의 가격 계산: '수익률(payoff) x 확률(probability)'
→ 확률이 반영된 미래의 기대수익을 현재가치로 할인하여 옵션의 가격을 결정
블랙-숄즈(-머튼) 모델
: 대표적인 옵션가격결정 모델

블랙-숄즈-머튼 모델의 가정
1. 기초자산인 주식의 배당금 지급 x
2. 거래비용, 세금, 공매도(short selling)의 제약이 없는 완전 시장(perfect market)이다
3. 무위험 이자율 & 기초자산 수익률의 '분산'은 옵션의 잔존기간 동안 변하지 않는다
4. 기초자산인 주식이 연속적으로 거래가 이루어지고 & 주가는 연속확률과정인 이토프로세스(=주가 움직임의 확률적 패턴에 대한 가정, 주가수익률은 정규분포를 따르고 주가는 로그정규분포를 따른다는 것)를 따른다
블랙숄즈 방정식 이해하기 (델타 헤징)
이미지 및 내용 출처: https://m.blog.naver.com/quantdaddy/221500026340
1. 주식과 같은 위험자산(Risky Asset)을 기초자산(S)으로 상정함
- GBM(Geometric Brownian Motion) 기반

2. 파생상품의 움직임 또한 기초자산처럼 추세항(Drift Term) & 변동성향(Diffusion Term)으로 나눌 수 있음
- 추세항: dt가 붙음
- 변동성향: dX가 붙음 (*X: 무작위성, Randomness, Risk)
추구방향: Risk 요인인 변동성향을 제거할 것(=dX를 없애자!)

3. Risk를 Hedge하는 합성(Π) 포트폴리오를 만들자:
옵션을 한 개 매수(Long) + 기초자산을 델타(Δ)만큼 매도(Short)

4. 포트폴리오가 무위험포트폴리오가 되도록(=옵션의 불확실성을 제거), 델타(Δ)를 결정해야 함

5. 식 전개의 결과,
무위험 포트폴리오에서의 델타(Δ)
= dX를 없애는 델타(Δ)
= 파생상품 변화분 / 기초자산 변화분
= 기초자산 가격에 대한 파생상품 가격의 민감도
오직 시간가치만을 가지고 있는 무위험 포트폴리오.
Delta Hedge: 해당 델타만큼 기초자산을 사거나 팔아서 포트폴리오의 위험(옵션의 불확실성)을 제거하는 것
🔎 델타 헤지를 이용하는 다른 사례: 전환사채 차익거래 https://lets-hci-la-ai-withme.tistory.com/206

6. 델타 헤지의 결과, 해당 포트폴리오는
→ 무위험수익률(r, Risk-free Rate)을 창출함
→ '무위험수익률만큼 가치가 증가하는 예금'같은 자산이 됨
→ 무위험차익거래 논리를 적용함으로써, 해당 무위험수익률 r을 계산해보자

결론: 블랙-숄즈 편미분 방정식
: 파생상품을 구성하는 기초자산 & 시간의 움직임에 따라, 파생상품의 움직임을 표현하게 됨, 이를 기반으로 옵션 가치 및 가격을 결정 🥹

블랙숄즈 옵션 공식 이해하기
1. 변수 이해하기
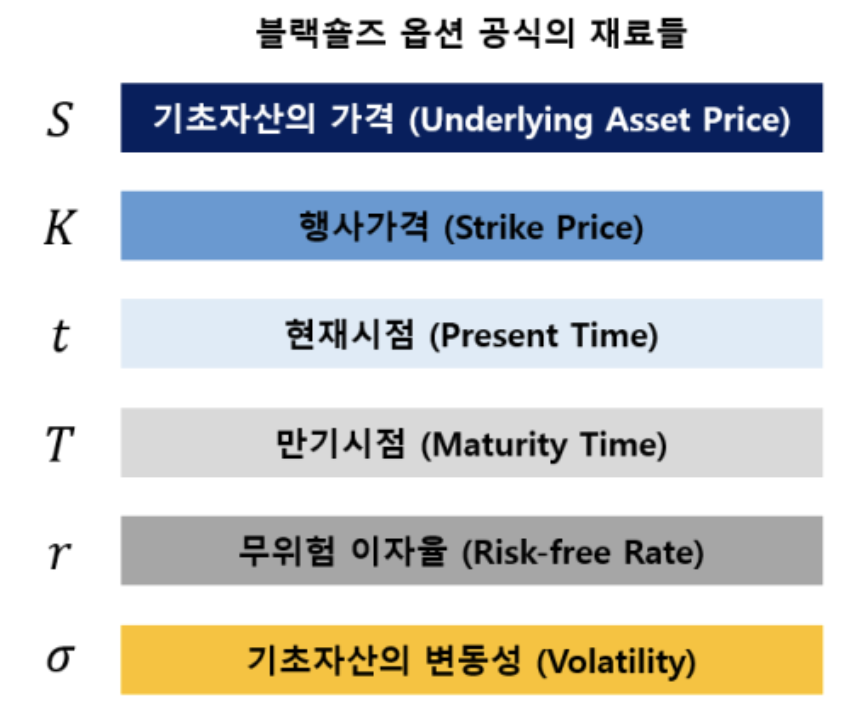
- 블랙숄즈 모델의 변수: 기초자산의 가격(S), 시간(t)
- 모델의 파라미터(모델 내부적으로 정해진 상수): 옵션의 행사가격(K), 만기시점(T), 무위험이자율(r), 기초자산의 변동성(시그마)
파생상품은 본질적으로 기초자산 가격변화 & 시간에 직접 영향을 받음, 나머지 파라미터는 이론적으로 상수 처리.
2. 블랙숄즈 옵션 공식: 콜옵션의 이론가, 풋옵션의 이론가(Theoretical Price)

N(x)?
표준정규분포에 대한 확률밀도함수(PDF)를 적분한 값인 누적분포함수(CDF, Cumulative Distribution Function)

유럽실 콜옵션 가격모형
C = S * N(d1) - {X / (1+r)**(T-t)} * N(d2)
기존 콜옵션 내재가치 공식인 Max(0, S - X) 에서
시장가치 S에는 '콜옵션의 델타'가 곱해지고, 행사가격 X에는 할인율 적용 & '콜옵션의 내가격 확률'이 곱해진 것이다
N(d1) = 콜옵션의 델타값
N(1-d1) = 1 - N(d1) = 풋옵션의 델타값
N(d2) = 콜옵션의 내가격 확률
내재 변동성 (~미래 변동성)
블랙-숄즈 공식에 따르면 주식 옵션의 가격은 변동성과 시장에서 관찰 가능한 5개의 요인에 의해 결정된다.

시장에서 관찰된 5개의 값을 블랙-숄즈 공식에 대입하면 유러피언 콜옵션의 가격은 변동성만의 함수로 표현된다.
(미래변동성을 의미하는 '내재변동성'만 다룸. 과거변동성)
이때 시장에서 거래되고 있는 옵션의 가격과 == 블랙-숄즈공식의 가격이 동일하게 되도록 하는 변동성을 : 내재변동성이라고 한다.
내재변동성은 옵션의 시장가격으로부터 추출된 값. 따라서, 현재 시장에서 예상하고 있는 미래의 상황을 잘 나타낸다.
변동성은 곧 위험을 의미하므로 옵션의 가격은 현재 시장에서 보고 있는 기초자산의 위험에 관한 정보를 제공해주는 역할을 한다고 말할 수 있다.
Refer to
https://terms.naver.com/entry.naver?docId=5668942&cid=60207&categoryId=60207
내재변동성
블랙-숄즈 공식에 따르면 주식 옵션의 가격은 변동성과 시장에서 관찰 가능한 5개의 요인에 의해 결정된다. 시장에서 관찰된 5개의 값을 블랙-숄즈 공식에 대입하면 유러피언 콜옵션의 가격은
terms.naver.com
블랙-숄즈-머튼 모델에서 활용하는 기초자산 모델링 기법 GBM
https://newindow.tistory.com/262
[금융공학] Geometric Brownian Motion 소개
1. GBM(Geometric Brownian Motion)이란? GBM은 주식의 기하학적 브라운 운동을 말하며, 2개의 parameter $\mu$(drift parameter)와 $\sigma$(volatility parameter)를 가진다. - $\mu$ (drift parameter) : 주식 가격의 트랜드를 반영
newindow.tistory.com
⭐️⭐️⭐️ 사실 아래 포스트를 보면 끝임..😁
https://m.blog.naver.com/quantdaddy/221500026340
금융공학 역사의 거대한 서막을 올린 블랙숄즈 방정식
# 세 명의 현자(賢者)가 세상을 바꾸다 1973년, 블랙(Fischer Black)과 숄즈(Myron Scholes), 그리고 ...
blog.naver.com
블랙-숄즈-머튼 모델의 역사 및 가치
'Finance > Basic' 카테고리의 다른 글
| [Finance] 신용파생상품 - CLN, CDO (0) | 2024.01.29 |
|---|---|
| [Finance] 채권차익거래(Fixed Income Arbitrage) (0) | 2024.01.29 |
| [Finance] 증권 / 유가증권 (0) | 2024.01.23 |
| [Finance] 신용파생상품(credit derivative) (1) | 2024.01.22 |
| [Finance] 채권 기본 (4) | 2024.01.22 |