바다에 퐁당 Ꙭ̮ ꉂ ◡̈⋆*

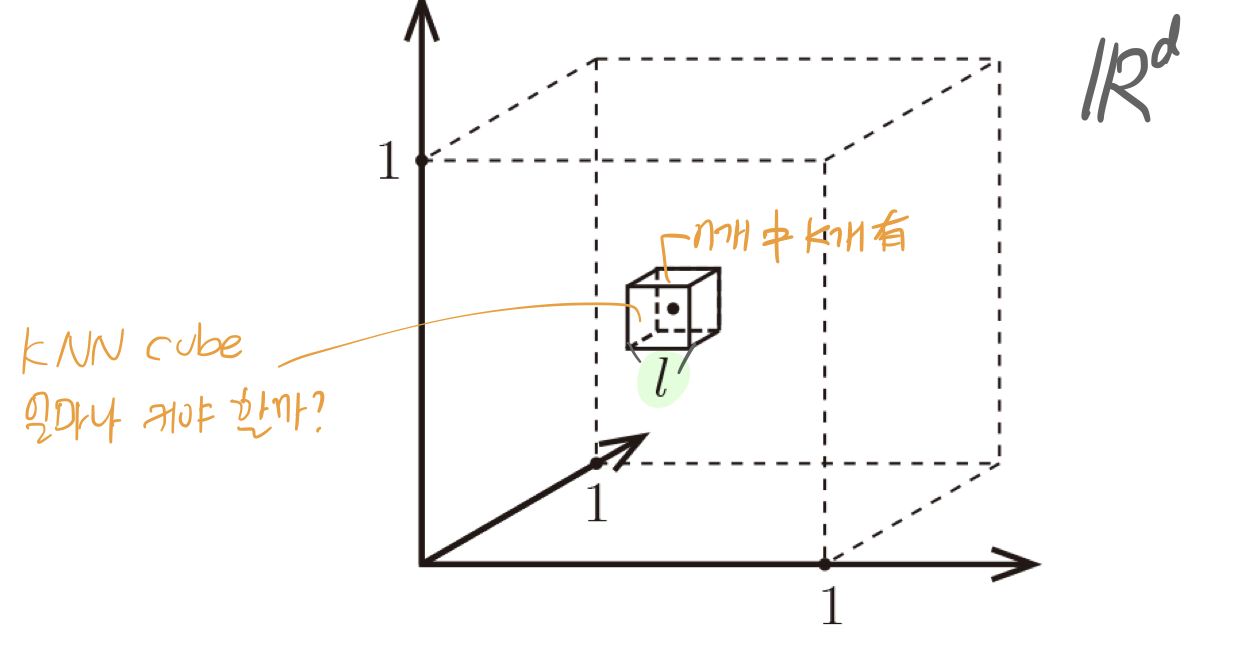
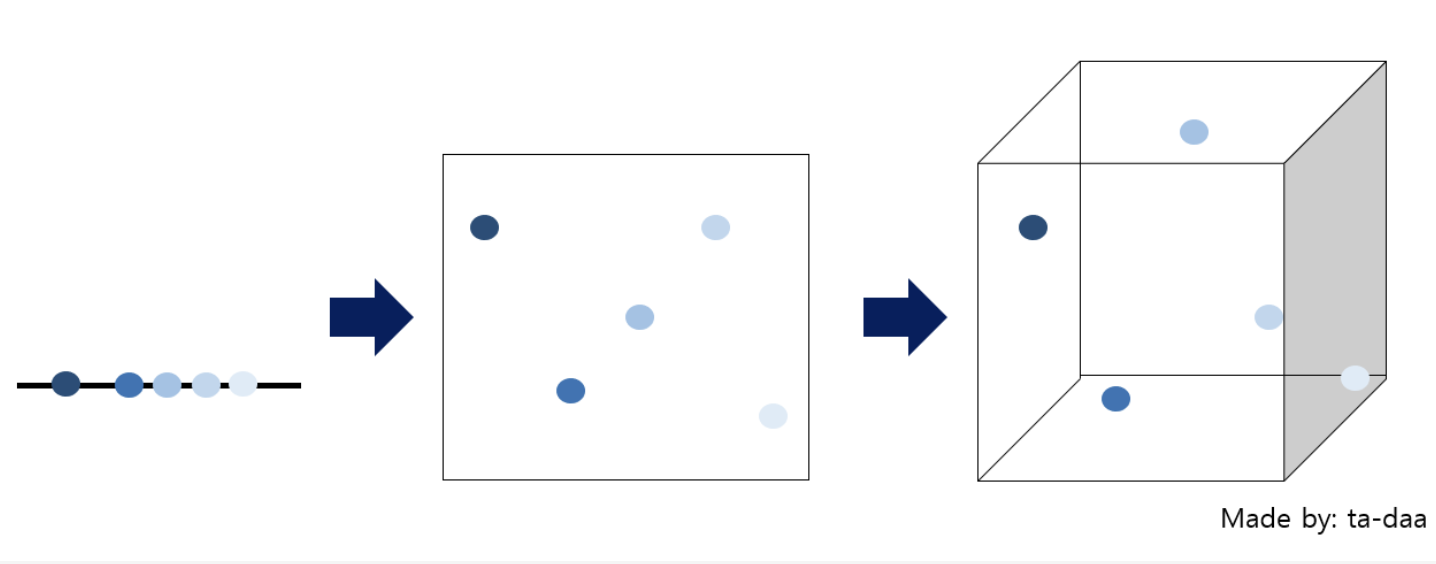
모집단(population)이란 정보를 얻고자 하는 관심 대상의 전체집합(집단 전체)

모수(population parameter)란 모집단 분포 특성을 규정 짓는 척도. 관심의 대상이 되는 모집단의 ‘대표값’.

표본(sample)은 모집단(population)의 부분집합

표본통계량(sample statistic)이란 표본의 몇몇 특징을 수치화한 값

확률변수(random variable): 확률현상에 기인해 결과값이 확률적으로 정해지는 변수

• 확률현상; 어떤 결과들이 나올지는 알지만 가능한 결과들 중 ‘어떤 결과가 나올지는 모르는’ 현상 (ex. 동전을 던졌을 때 나오는 면)
• 확률변수는 상수가 아닌 ‘변수’이다. 우리 주변에 확률적인 현상이 존재할때, 확률변수는 확률적으로 정해지는 것이고, 현상에 따라 변화할 수 있기 때문이다.
• 확률변수의 예시: 확률변수 X = 100원짜리 동전을 한 번 던졌을 때 이순신 장군이 나오는 횟수, P(X) = 1/2

확률분포(probability distribution)은 확률변수가 ‘특정한 값을 가질 확률’을 나타내는 ‘함수’

• 확률분포의 종류: 확률변수의 종류에 따라 둘로 나뉨
  • 이산확률분포(discrete p.b.): 이산확률(확률변수가 가질 수 있는 ‘값의 개수를 셀 수 있는’ 경우)의 확률분포. (e.g. X=주사위를 던져서 나오는 눈의 개수일 때 1,2,3,4,5,6)
    • 확률질량함수(probability mass function, pmf): 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수 (e.g. X=주사위를 던져서 나오는 눈의 개수, f_x(1) = P(X=1) = 1/6)
    • 이산확률분포의 종류: 베르누이분포와 이항분포, 기하분포와 음이항분포, 초기하분포, 포아송분포)
  • 연속확률분포(continuous p.b.): 연속확률변수(확률변수가 가질 수 있는 ‘값의 개수를 셀 수 없는’ 경우)의 확률분포 (e.g X=중학교 학생의 키)
    • 확률밀도함수(probability density function, pdf): 연속확률변수가 ‘특정 구간’에 포함될 확률
    • 누적분포함수(cumulative distribution function, pdf): 주어진 확률 변수가 특정 값보다 작거나 같은 확률
    • 연속확률분포의 종류: 정규분포, 감마분포, 지수분포, 카이제곱분포, 베타분포, 균일분포

독립항등분포(iid, independent and identically distributed): 두 개 이상의 확률변수를 고려할 때, 각 변수들이 통계적으로 독립이고, 동일한 확률분포를 가지고 있을 때, 독립항등분포를 따른다고 함.

베타분포(Beta Distribution): 두 매개변수 α와 β에 따라 [0, 1] 구간에서 정의 되는 연속확률분포

*α와 β; 분표의 형태를 결정짓는 모수

• 쓰임새: 베이지안에서 사전확률을 가정할때 베타분포를 가정. (모수에 따라 다양한 형태로 변형 가능하기 때문, 사전정보가 없는 상황에서는 베타분포를 많이 가정한다고 함)
• 베타함수를 이용

Reference:

https://losskatsu.github.io/statistics/betadist/#

이분탐색의 사용 조건: 리스트에 원소가 이미 '잘 정렬되어 있을 때'

• 이진 탐색(이분 탐색) 알고리즘은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법.
• 이진 탐색은 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다.
• 변수 3개(start, end, mid)를 사용하여 탐색한다. 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 것이 이진 탐색의 과정.

https://velog.io/@kimdukbae/%EC%9D%B4%EB%B6%84-%ED%83%90%EC%83%89-%EC%9D%B4%EC%A7%84-%ED%83%90%EC%83%89-Binary-Search

# 재귀 함수로 구현한 이진 탐색
def binary_search(array, target, start, end):
    if start > end:
        return None
    mid = (start + end) // 2

    # 원하는 값 찾은 경우 인덱스 반환
    if array[mid] == target:
        return mid
    # 원하는 값이 중간점의 값보다 작은 경우 왼쪽 부분(절반의 왼쪽 부분) 확인
    elif array[mid] > target:
        return binary_search(array, target, start, mid - 1)
    # 원하는 값이 중간점의 값보다 큰 경우 오른쪽 부분(절반의 오른쪽 부분) 확인
    else:
        return binary_search(array, target, mid + 1, end)

# 반복문으로 구현한 이진 탐색
def binary_search(array, target, start, end):
    while start <= end:
        mid = (start + end) // 2

        # 원하는 값 찾은 경우 인덱스 반환
        if array[mid] == target:
            return mid
        # 원하는 값이 중간점의 값보다 작은 경우 왼쪽 부분(절반의 왼쪽 부분) 확인
        elif array[mid] > target:
            end = mid - 1
        # 원하는 값이 중간점의 값보다 큰 경우 오른쪽 부분(절반의 오른쪽 부분) 확인
        else:
            start = mid + 1

    return None

https://school.programmers.co.kr/learn/courses/30/lessons/81302

문제 개요

<Input>

Places: ‘자리에 앉아있는 응시자들의 정보와 대기실 구조’를 대기실별로 담은 2차원 문자열 배열.

*대기실은 5개이며, 각 대기실은 5x5 크기

*P(응시자가 앉아있는 자리),O(빈 테이블),X(파티션)로 이루어진 문자열

*Rule

1. 거리두기를 위하여 응시자들 끼리는 맨해튼 거리1가 2 이하로 앉지 말아 주세요.
2. 단 응시자가 앉아있는 자리 사이가 파티션으로 막혀 있을 경우에는 허용합니다.

예: [["POOOP", "OXXOX", "OPXPX", "OOXOX", "POXXP"], ["POOPX", "OXPXP", "PXXXO", "OXXXO", "OOOPP"], ["PXOPX", "OXOXP", "OXPOX", "OXXOP", "PXPOX"], ["OOOXX", "XOOOX", "OOOXX", "OXOOX", "OOOOO"], ["PXPXP", "XPXPX", "PXPXP", "XPXPX", "PXPXP"]]

<Output>

각 대기실별로 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 배열에 담아.

예: [1, 0, 1, 1, 1]

내 코드

못생긴 코드ㅡ... 코드가 왜 이렇게 길지? ^__^

ㅎㅎ

모범코드 보면서 공부해야겠다..

from collections import deque
def solution(places):
    
    answer = [1 for _ in range(5)]

    next_i, next_j = [-1, 0, 0, 1], [0, -1, 1, 0]
    doub_i, doub_j = [-2, 0, 0, 2], [0, -2, 2, 0]
    cross_i, cross_j = [-1, -1, 1, 1], [-1, 1, -1, 1]

    cnt = -1
      
    for place in places:
        cnt += 1
        place = list(map(list, place))
        p_lst = deque() #각 대기실에서 P가 있는 좌표 리스트
        for i, row in enumerate(place):
            for j, col in enumerate(row):
                if place[i][j] == 'P':
                    p_lst.append((i,j))
                    
        loopbreak = False
        while p_lst and (loopbreak == False):
            (i,j) = p_lst.popleft() #현재 중심이 되는 좌표 (i,j)
            for k in range(4): #위반 케이스 1
                ci = i + next_i[k]
                cj = j + next_j[k]
                
                if ci <0 or ci>4 or cj<0 or cj>4:
                    continue
                if place[ci][cj] == 'P':
                    answer[cnt] = 0
                    loopbreak = True
                    break
                
            if loopbreak == True: break
            for k in range(4): #위반 케이스 2
                ci = i + doub_i[k]
                cj = j + doub_j[k]
                if ci <0 or ci>4 or cj<0 or cj>4:
                    continue
                if place[ci][cj] == 'P':
                    if place[i + next_i[k]][j + next_j[k]] == "O":
                        answer[cnt] = 0
                        loopbreak = True
                        break
            if loopbreak == True: break
            for k in range(4): #위반 케이스 3
                ci = i + cross_i[k]
                cj = j + cross_j[k]
                if ci <0 or ci>4 or cj<0 or cj>4:
                    continue
                if place[ci][cj] == 'P':
                    if k == 0:
                        if place[i-1][j]=='X' and place[i][j-1]=='X': continue   
                    elif k == 1:
                        if place[i-1][j]=='X' and place[i][j+1]=='X': continue  
                    elif k == 2:
                        if place[i][j-1]=='X' and place[i+1][j]=='X': continue
                    elif k == 3:
                        if place[i][j+1]=='X' and place[i+1][j]=='X': continue
                    
                    answer[cnt] = 0
                    loopbreak = True
                    break

    return(answer)

• 테케 3, 8, 31번 오답의 반례 : 'POP'가 포함된 경우 '0'을 반환해야 한다
• answer의 default 원소로 1 채워놓고, 위반하는 경우=>  0으로 바꿈 & 다음 place로 바로 이동(기존 반복문 break)
• visited 리스트 이용해서 좀 더 효율적으로 구현했었는데 => 딱히 효과가 없다 ^__^ BFS 개념에 집착하지 말자,,

• 이중 반복문 빠져나오는 법: loopbreak과 같은 변수 사용,,
• 반복문 continue 개념

https://velog.io/@banana/break-continue%EB%A1%9C-%EB%B0%98%EB%B3%B5%EB%AC%B8-%EC%A0%9C%EC%96%B4%ED%95%98%EA%B8%B0

• 상하좌우 살피는 예쁜 코드 [-1,0,0,1] 등 사용해서 짰는데 (왜 전체 코드가 이리 장황할까?)

그래도 아래 코드는 유용하게 사용하쟈~

dx = [1,-1,0,0]
dy = [0,0,1,-1]

for k in range(4):
            cx = i + dx[k]
            cy = j + dy[k]
            if cx < 0 or cx >= N or cy < 0 or cy >= M:
                continue
            if arr[cx][cy] != 1:
                graph[i*M+j].append(cx*M+cy)

내적

- np.dot(a, b)

노름

- np.linalg.norm(a) #default: l2 norm

- np.linalg.norm(a,1) # l1 norm <->  np.ingalg.norm(a,2) # l2 norm

유클리드 거리 (a, b 두 개의 벡터가 있다고 할 때)

- np.linalg.norm(a-b)

넘파이에서 제공하는 np.arange

np.repeat & np.tile => 아래 링크에 정리 굿!

https://yeko90.tistory.com/entry/%EB%84%98%ED%8C%8C%EC%9D%B4-%EA%B8%B0%EC%B4%88-nprepeat-nptile-%EB%B0%B0%EC%97%B4-%EB%B0%98%EB%B3%B5-array-%EB%B3%B5%EC%82%AC

Reference

https://jimmy-ai.tistory.com/45

np.reshape(대상, (size))

https://yganalyst.github.io/data_handling/memo_5/

유클리드 거리 결과 담은 matrix 계산하기

https://pbj0812.tistory.com/329

원문 출처. 아래 내용을 인용하여 정리함 (아주 잘 정리되어있으니 대추천!!)

https://agronomy4future.org/?p=2295 

https://agronomy4future.org/?p=9774 

1. R-squared (결정계수)

정의: (단순 선형 회귀분석에서) 전체 제곱합 중에서 회귀 제곱합이 차지하는 비율

- R-squared가 높을 수록 "우리가 추정한 회귀 모형이 더 적합하다"고 볼 수 있음.

*x에 반응하는 y값이 거의 같은 값(constant)일 경우: R-squared 는 극도로 낮아짐

* 만일 y값이 완전 다 똑같다면 R-squared 는 계산되지 않음

SST = SSR + SSE

Data = Fit + Error

Data = Regression + Residual

SST = Sum of Squares Total; [실제 개별 y값에서 그 y 값 전체의 평균을 뺀값 (yi – ȳ)]의 제곱합
SSR = Sum of Squares due to regression; [예측된 개별 y 값에서 실제 y 값 전체의 평균을 뺀 값 (ŷi-ȳ)]의 제곱합
SSE = Sum of Squared Error; [실제 개별 y 값에서 예측된 개별 y 값을 뺀 값 (yi-ŷi)]의 제곱합

*ANOVA: ANalysis Of VAriance (분산분석), 각 데이터의 분산에 대한 해석.

- 상관계수(r)의 제곱 == R-squared 값

=> 결정계수 R-squared에 루트 == 상관계수 값!

2. 공분산(Covariance)

2.1 공분산 개념 이해의 필요성

: 변수 간 상관관계를 분석하는 '상관분석'이 '공분산' 개념을 base로 함. => 상관분석에 앞서 공분산 이해가 선행!

: 그러나, 이따 다루겠지만, 상관계수량와 공분산량이 아주 직접적인 상관성을 갖지는 않음,,

그저 상관계수 공식에서 공분산 공식이 사용될 뿐. (positive인지 negative인지 정도는 구분 가능)

2.2 공분산

: 두 변수간의 선형관계를 나타내는 값. 

- 하나의 변수가 증가 혹은 감소함에 따라 ➡️ 다른 변수는 어떻게 그 증감에 반응하는지에 대한 측도

2.3 공분산 계산

- [x의 개별 편차(xi - x̄) X y의 개별편차(yi - ȳ)]의 sum / 자유도 (n-1)

- 우리 데이터가 모집단이 아닌 표본집단이면 n이 아닌 n-1로 나눔

2.4 공분산 해석

*공분산은 제곱합이 아니므로, 음수가 나올 수 있음

- 공분산이 양수; 두 변수가 양의 상관관계

- 공분산이 음수; 두 변수가 음의 상관관계

2.5 공분산은 클수록 좋을까?(=공분산이 클수록 상관계수가 높을까?)

Q. “공분산은 무조건 커야 좋은 것일까?”

A. 공분산의 크기가 아니라 변수의 표준편차에 따라 달라진다” 라고 하는게 더 정확한 표현.

2.5.1 상관계수 r 계산

*상관계수 공식을 보면 여러 공식이 존재하는 것 같지만 사실은 모두 {공분산 / x, y 표준편차의 곱} 의 공식에서 다 수정된 것들.

2.5.2 <공분산과 상관계수 r의 관계> 결론

2.5.3 왜 실제로는, 공분산값이 아닌 상관계수 r값을 주요 지표로 사용하는가?

공분산은 두 편차의 곱을 자유도로 나눈것이기 때문에 원래의 측정치 보다는 무척이나 큰 값

분산의 경우, 원래의 값의 크기로 돌리기 위해 루트를 씌운 표준편차를 사용.

공분산도 마찬가지로 원래의 값 크기로 돌려야 하므로, 공분산에 x, y 표준편차의 곱을 나눠주어야 하고, 그 값이 상관계수 r.

양질의 자료 제공해주신 agronomy4future님께 다시 한번 감사합니다:)

*Covariance Matrix

https://www.youtube.com/watch?v=152tSYtiQbw 

1. GPU(Graphics Processing Unit)

CPU보다 효율적인 코어로 구성되어 대규모 데이터를 병렬로 빠르게 처리할 수 있도록 최적화된 '컴퓨팅 자원'

예전에는, 컴퓨터 연산 시 CPU & RAM에 의존함

CPU가 보유한 코어 개수만큼 Multi-Core를 이용하여 연산 수행

(pytorch나 tensorflow 에서, data loader 파트에서, core 갯수를 주고 데이터 loading 하는 부분이 여기에 속함)

1. GPU 서버

(대용량 연산에 장점을 가진) GPU를 활용한 '인프라'

2. GPU 클라우드

기존 문제 상황

- GPU를 직접 구매 또는 대여하여 서버를 구축하는 것은 큰 부담이 될 수 있음

- GPU 자원은 CPU와는 달리 여러 명의 사용자가 동시에 이용하기 위해서는 사전에 분배 및 할당 과정이 필요한데, 이를 관리하기 위한 소프트웨어의 개발 및 운영이 추가적으로 필요함.

GPU 클라우드를 통한 해결

-  여러 개의 GPU를 필요에 따라 구매하여 동시에 사용

- 고급 인프라를 구축할 필요 없이 GPU의 처리 능력을 기업과 개발자들이 편리하게 사용할 수 있게 됨

종류

- 구글 코랩

- Paperspace

- Jarvis Labs 등.

3. CUDA

:  NVIDIA에서 개발한 GPU 개발 툴 => 많은 양의 연산을 동시에 처리하는 것이 목표

- NVIDIA에서  많은 연구자들이 딥러닝에 사용할 수 있도록, 쉽게 설치할 수 있도록 오픈하였다.

- 현재는 nvidia-driver, CUDA, CUDNN만 설치하면 딥러닝을 쉽게 사용할 수 있다.

2. GPU 서버 접속

1. 서버란?: https://youtu.be/R0YJ-r-qLNE

2. ssh-key란?: SSH(Secure Shell)는 원격지 호스트 컴퓨터에 접속하기 위해 사용되는 인터넷 프로토콜.

- 서버에 접속할때 비밀번호 대신 key를 제출하는 방식이다. 비밀번호보다 높은 수준의 보안요건을 필요로 할때 사용된다.

- 공개키(public key)와 비공개키(private key)로 이루어지는데 이 두개의 관계를 이해하는 것이 SSH Key를 이해하는데 핵심이다. 키를 생성하면 공개키와 비공개키가 만들어진다. 이 중에 비공개키는 로컬 머신에 위치해야 하고, 공개키는 리모트 머신에 위치해야 한다.(로컬 머신은 SSH Client, 원격 머신은 SSH Server가 설치된 컴퓨터를 의미한다) SSH 접속을 시도하면 SSH Client가 로컬 머신의 비공개키와 원격 머신의 비공개키를 비교해서 둘이 일치하는지를 확인한다.

인용

https://elice.io/newsroom/gpu_definition_and_exampless

https://kaen2891.tistory.com/20

https://velog.io/@hyeseong-dev/%EB%A6%AC%EB%88%85%EC%8A%A4-ssh%EB%9E%80

공부한 자료

https://daebaq27.tistory.com/82

https://veggie-garden.tistory.com/42

https://school.programmers.co.kr/learn/courses/30/lessons/43164#qna

풀이 코드

from collections import deque

def solution(tickets):
    # 주어진 항공권은 모두 사용
    # 주어진 공항수 꽤 많음
    tickets.sort()
    dic = {}
    for tic in tickets:
        if tuple(tic) not in dic.keys():
            dic[tuple(tic)] = 1
        else:
            dic[tuple(tic)] +=1

    for root in [x for x in tickets if x[0]=="ICN"]:
        deq = deque()
        deq.append([root]) #dic, visited list
        while deq:
            visited = deq.popleft() #현재 다루는 dic과 그것이 사용된 횟수
            for tic in tickets:
                if (visited[-1][1] == tic[0]) and (visited.count(tic) < dic[tuple(tic)]):
                    if len(visited)+1 == len(tickets):
                        mod = [x[1] for x in visited+[tic]]
                        mod.insert(0, visited[0][0])
                        # print(mod)
                        return mod
                    else:
                        deq.append(visited+[tic])


    return #방문하는 공항 경로 #알파벳 순서가 앞서는 경로

• 알파벳 정렬은, 처음부터 input 리스트 'tickets'을 sort시키고 시작하면 해결된다.
• DFS의 특이한 버전이었다. 
  
  - input에 동일한 티켓이 여러 장 포함될 가능성이 있다. 따라서 다음 탐색 노드를 추가할 때 visited 존재 여부로 결정해서는 안 된다. (이미 방문하여 visited에 존재하지만, 탐색 가능한 것이 여전히 남아 있을 수 있다)
     ✂︎ 미리 counter dictionary를 생성하고, visited가 포함하는 개수와 비교해야 한다:
          visited.count(tic) < dic[tuple(tic)]
  
  - 지금까지 경로 데이터를 모두 가지고 있어야 한다
     ✂︎ deque의 원소 자체를 visited 리스트로 저장
     ✂︎ deep 하게 for문 돌 때, 기존 visited에 현재 탐색 원소를 append하여 기존 visited의 몸뚱아리를 키우는 것이 아니다.
         별도의 리스트(visited + [tic])로 만들어 그것을 deque에 append한다.
         (효율성 괜찮나..? 싶었으나 더 간단한 방법이 떠오르지 않음)
  
  
• 리스트를 원소로 가지는 리스트의 처리는 Unhashable error에 주의해야 한다. 나는 dictionary 생성 및 count를 위해 각 리스트 원소를 tuple로 변환하였다.
  https://daewonyoon.tistory.com/363 

• 트리 형태로 시각화한 후 수도코드 짜는 게 훨씬 수월할 듯.

https://www.acmicpc.net/problem/5397

문제 개요

비밀번호 창에서 입력한 키가 주어졌을 때, 강산이의 비밀번호를 알아내는 프로그램.

입력한 키: 알파벳 대문자, 소문자, 숫자, 백스페이스, 화살표

'-' : 백스페이스 (커서 바로 앞에 있는 글자를 지움(글자가 있으면))

‘<‘: 커서를 왼쪽으로 1만큼 움직임 (움직일 수 있다면)

‘>’: 커서를 오른쪽으로 1만큼 움직임 (움직일 수 있다면)

나머지 문자는 비밀번호의 일부. (나중에 백스페이스를 통해서 지울 수 있음)

Input

첫째 줄에 테스트 케이스의 개수

각 테스트 케이스는 한줄로 & 입력한 순서대로 길이가 L인 문자열 (input이 매우 큼 => 효율성이 중요함)

<<BP<A>>Cd-

Output

비밀번호를 출력한다. (비밀번호의 길이는 항상 0보다 크다.)

문제 풀이

class Node:
    def __init__(self, x):
        self.item = x
        self.before = None
        self.next = None

class LinkedList:
    def __init__(self) -> None:
        dummy = Node(-1)
        self.head = dummy
        self.cursor = self.head
    
    def append(self, x):
        new = Node(x)
        new.next = self.cursor.next
        new.before = self.cursor # type: ignore
        if self.cursor.next != None:
            self.cursor.next.before = new
        self.cursor.next = new # type: ignore
        self.cursor = new
        
    def delete(self):
        if self.cursor == self.head: return
        self.cursor.before.next = self.cursor.next
        if self.cursor.next != None:
            self.cursor.next.before = self.cursor.before
        self.cursor = self.cursor.before
    
    def left(self):
        if self.cursor == self.head: return
        self.cursor = self.cursor.before
        
    def right(self):
        if self.cursor.next == None: return
        self.cursor = self.cursor.next
        
    
L = int(input())
inputs = []
for _ in range(L):
    inputs.append(input())

for cmd in inputs:
    link_lst = LinkedList()
    answer = []
    for i in range(len(cmd)):
        if cmd[i] == "-":
            link_lst.delete()
        elif cmd[i] == "<":
            link_lst.left()
        elif cmd[i] == ">":
            link_lst.right()
        else:
            link_lst.append(cmd[i])

    crt = link_lst.head
    while crt.next != None:
        crt = crt.next
        answer.append(crt.item)
    
    print(''.join(answer))

=> cursor의 위치를 정확히 정의해야 함!

https://school.programmers.co.kr/learn/courses/30/lessons/81303

양방향 Linked List에 구현 로직이 동일한 것 같은데

왜 내 코드는 효율성 테스트를 통과하지 못하는 거지..?

비교해서 효율성 개선 방법 찾아내야겠다 ㅠㅠ

효율성 통과 코드

class Node:
    def __init__(self,data=None,prev=None,next=None):
        self.prev= prev
        self.data= data
        self.next= next
class DoubleLinkedList:
    def __init__(self,data=None):
        # for easy calculate at end set two dummy head_dummy and tail_dummy
        self.head = Node()
        self.tail = Node()
        # link two dummy
        self.head.next = self.tail
        self.tail.prev = self.head
        self.current_ptr = self.head
        self.delete_array = []


    def init_insert(self,data):
        new_node = Node(data)
        # get tail-1 node
        node = self.tail.prev
        node.next = new_node
        
        new_node.prev = node
        new_node.next = self.tail
        
        self.tail.prev = new_node
    
    def set_current_ptr(self, num):
        for i in range(num+1):
            self.current_ptr = self.current_ptr.next

    
    def c_instruction(self):
        self.before_ptr = self.current_ptr
        self.current_ptr = self.current_ptr.next
        if(self.current_ptr == self.tail):
            self.current_ptr = self.current_ptr.prev
            self.current_ptr = self.current_ptr.prev
        # delete!!
        self.delete_array.append(self.before_ptr)
        # modify linked list
        self.before_ptr.prev.next = self.before_ptr.next
        self.before_ptr.next.prev = self.before_ptr.prev
        
    def u_instruction(self, num):
        for i in range(num):
            self.current_ptr = self.current_ptr.prev
    
    def d_instruction(self, num):
        for i in range(num):
            self.current_ptr = self.current_ptr.next
    
    def z_instruction(self):
        node_to_z = self.delete_array.pop(-1)
        node_to_z.prev.next = node_to_z
        node_to_z.next.prev = node_to_z
    def return_del_array(self):
        to_return = []
        for i in range(len(self.delete_array)):
            to_return.append(self.delete_array[i].data)
        return to_return

            
def solution(n,k,cmd):
    answer_string = ["O"]*n
    my_list = DoubleLinkedList()
    for i in list(range(n)):
        my_list.init_insert(i)
    my_list.set_current_ptr(k)
    for instruction in cmd: 
        if instruction[0] == "U":
            instruction_list = instruction.split()
            move_cnt = int(instruction_list[1])
            my_list.u_instruction(move_cnt)
        elif instruction[0] == "D":
            instruction_list = instruction.split()
            move_cnt = int(instruction_list[1])
            my_list.d_instruction(move_cnt)
        elif instruction[0] == "C":
            my_list.c_instruction()
        elif instruction[0] == "Z":
            my_list.z_instruction()
    deleted_element = my_list.return_del_array()
    for element in deleted_element:
        answer_string[element] = "X"
    return ''.join(answer_string)

효율성 통과하지 못하는 코드

class Node:
        def __init__(self, x):
            self.item = x
            self.before = None
            self.next = None

class LinkedList:
    def __init__(self):
        dummy = Node(-1)
        self.bins = [dummy]
        self.tail = dummy
        self.current = None

    def append(self, x):
        new = Node(x)
        self.tail.next = new
        new.before = self.tail
        self.tail = new
        return new
    
    def up(self, x):
        for _ in range(x):
            self.current = self.current.before
        
    def down(self, x):
        for _ in range(x):
            self.current = self.current.next
    
    def delete(self):
        self.bins.append(self.current)
        
        if self.current.next == None:
            self.current = self.current.before
            self.current.next = None

        else:
            self.current.before.next = self.current.next
            self.current.next.before = self.current.before
            self.current = self.current.next
        
        
    def restore(self):
        if self.bins:
            res_data = self.bins.pop()
            res_data.before.next = res_data
            if res_data.next != None:
                res_data.next.before = res_data
        
    
    def return_del(self):
        del_lst = [x.item for x in self.bins]
        return del_lst


def solution(n, k, cmd):
    answer = [i for i in range(n)] #비효율의 원인
    link_lst = LinkedList()
    
    for i in answer:
        if i == k:
            link_lst.current = link_lst.append(i)
        else:
            link_lst.append(i)

    for x in cmd:
        
        if x[0] == "U":
            link_lst.up(int(x[2:]))
        
        elif x[0] == "D":
            link_lst.down(int(x[2:]))
        
        elif x[0] == "C":
            link_lst.delete()
        
        else:
            link_lst.restore()
    
    del_lst = link_lst.return_del()
    final = ["O" if x not in del_lst else "X" for x in answer] #비효율의 가장 큰 원인: O(N)
    final = ''.join(final)
    # print(final)
    return final

• 양방향 LinkedList까지 로직 참 좋았다 ! 
• input의 크기가 무지막지하게 크다는 사실을 기억해야 한다
• input 처리에 대한 단순한 코드때문에 => 눈덩이처럼 커진 비효율이,,,!!!!!!!
• input의 value는 사실 중요하지 않다. 서로가 '중복되지 않음'만 확인되면 된다.
  나는 처음에 각 Node를 생성하고 해당 노드의 value(Node.item)가 저장된 answer 리스트를 따로 생성했었다.
  그러나, integer로 채워진 answer 리스트를 임의로 생성할 필요가 없었다. 생성하면 무조건 비효율 문제가 발생하게 된다
  => answer 생성: O(N) + final 생성: O(N) = 2*O(N)
  이미 각 Node들의 item 값은 서로 다르기때문에 '중복되지 않음'의 속성이 반영되어 있다.
• 초반에 append한 각 Node의 value 값과 idx 값이 동일함을 이용하여 answer 리스트의 원소로 미리 "O"를 넣어둔다
• 마지막에 del_lst의 item값을 answer의 idx값으로 이용하여 answer 리스트에서 해당 idx의 값을 "X"로 바꾸어준다
  => final 리스트 따로 생성하지 않음! answer 리스트 내에서 변형.
  => O(N) + O(len(del_lst))
  => 이때 N보다 del_lst가 작으므로, N이 무지막지한 크기인 본 문제에서 효율성을 크게 높일 수 있다..!!

최종 효율성 통과 코드

class Node:
        def __init__(self, x):
            self.item = x
            self.before = None
            self.next = None

class LinkedList:
    def __init__(self):
        dummy = Node(-1)
        self.bins = [dummy]
        self.tail = dummy
        self.current = None

    def append(self, x):
        new = Node(x)
        self.tail.next = new
        new.before = self.tail
        self.tail = new
        return new
    
    def up(self, x):
        for _ in range(x):
            self.current = self.current.before
        
    def down(self, x):
        for _ in range(x):
            self.current = self.current.next
    
    def delete(self):
        self.bins.append(self.current)
        
        if self.current.next == None:
            self.current = self.current.before
            self.current.next = None

        else:
            self.current.before.next = self.current.next
            self.current.next.before = self.current.before
            self.current = self.current.next
        
        
    def restore(self):
        if self.bins:
            res_data = self.bins.pop()
            res_data.before.next = res_data
            if res_data.next != None:
                res_data.next.before = res_data
        
    
    def return_del(self):
        del_lst = [x.item for x in self.bins]
        return del_lst


def solution(n, k, cmd):
    answer = ["O" for _ in range(n)] #효율 개선
    link_lst = LinkedList()
    
    for i in range(len(answer)):
        if i == k:
            link_lst.current = link_lst.append(i)
        else:
            link_lst.append(i)

    for x in cmd:
        
        if x[0] == "U":
            link_lst.up(int(x[2:]))
        
        elif x[0] == "D":
            link_lst.down(int(x[2:]))
        
        elif x[0] == "C":
            link_lst.delete()
        
        else:
            link_lst.restore()
    
    del_lst = link_lst.return_del()
    for x in del_lst[1:]: #주의
        answer[x] = "X" #효율 개선
        
    answer = ''.join(answer)
    print(answer)
    return answer

너무 잘 정리된 LinkedList 개념

https://wayhome25.github.io/cs/2017/04/17/cs-19/

표 편집 솔루션에 대한 좋은 레퍼런스

https://latte-is-horse.tistory.com/329

https://life318.tistory.com/2

유용한 링크

https://blockdmask.tistory.com/443

https://blockdmask.tistory.com/445

부모클래스의 생성자를 상속받으려면 => 자식클래스의 생성자 __init__ 아래 줄에 super 사용해야 함.

반면, 부모클래스의 메소드를 상속받으려면, 자식클래스 괄호 안에 부모클래스 언급만 하고, super 할 것  없음.

만약 메소드를 변형하고자 한다면 그게 곧 '오버라이딩' 한다는 거임.그때 def 하면 됨.

이외 자식클래스에만 별도로 추가로 함수 정의하고자 한다면 def 하고.

KNN alogrithm ∈ Classifiers

1. assumption: Similar Inputs have Similar Outputs

2. Classification rule: For a test input x, assign the most common label amongst its k most similar training inputs

3. 특징

3.1 Distance metric: metric이 label similarity & semantically meaningful notion을 잘 반영할 때 KNN의 효과가 높아짐
- 흔히 Minkowski distance를 사용

3.2 n(=train data points의 개수)가 커질수록, kNN은 더욱 정확해짐 (물론 느려짐)

3.3 d(=각 data의 feature 개수 = 차원)이 너무 커지면, 차원의 저주(curse of dimensionality) 발생하여 모델 성능이 저하됨

- 물론, 차원 수가 늘어나도 그것에 영향을 덜 받는, Data with low dim structure가 있긴 함(digits / 인간 얼굴), 그러나 특이 케이스.

차원의 저주(curse of dimensionality) (in kNN)

Description

• data의 차원 수; d => d-dimensional space에 매핑됨
• train data가 n개
• hyper-cube: kNN points가 모두 포함된 smallest cube
• l = hyper-cube 모서리 길이
•  

차원의 저주 발생 조건

(학습 데이터 수에 비해) 차원 수가 커질수록 = n에 비해 d값이 너무 커지면

* 차원이 증가한다고 반드시 차원의 저주가 발생하는 건 X. number of train data보다 number of features가 많아지는 경우에만 발생

- data points 간 모든 distances가 아주 커지고 & concentrate within a very small range

   → 차원이 증가할수록 빈 공간이 많아진다.

   → 개별 차원 내에서 학습할 데이터 수가 적어짐

같은 데이터지만 1차원에서는 데이터 밀도가 촘촘했던 것이 2차원, 3차원으로 차원이 커질수록 점점 데이터 간 거리가 멀어짐. 차원이 증가하면 빈 공간이 생기는데 빈 공간은 컴퓨터에서 0으로 채워진 공간. 즉, 정보가 없는 공간이기 때문에 빈 공간이 많을수록 학습 시켰을 때 모델 성능이 저하. ∵ 차원 별 충분한 데이터 수가 존재하지 않으면 과적합이 될 수 있음. 알고리즘 모델링 과정에서 저장 공간과 처리 시간이 불필요하게 증가함.

고차원 공간은 이렇게 공간이 많아 훈련 데이터가 서로 멀리 떨어져 있고 새로운 샘플도 훈련 샘플과 멀리 떨어져 있을 가능성이 높다. 

   → 이것을 극복하기 위한 두 가지 방법

       (1) train data를 늘리려면, 기하급수적으로 많은 양의 데이터가 필요함: 거의 불가능

       (2) 차원 축소 알고리즘: 현실적

            - PCA, LDA, LLE, MDS, t-SNE etc.

- 반면, points와 hyperplane 간 distance는 stable하게 유지되거나 & 아주 작은 변화
   → 모든 points가 hyperplane에 매우 가까워져서, classification outcome을 변화시키기 위해 input을 약간 교란시킬 수도 있음

   → hyperplane을 사용하는 classifier ; Perceptron, SVMs, ...

이미지 & 내용 Reference

https://datapedia.tistory.com/15

https://for-my-wealthy-life.tistory.com/40

https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote02_kNN.html

어려운 기호 발견할 때마다 업데이트할 예정 !! 😍

https://ko.wikipedia.org/wiki/%EC%88%98%ED%95%99_%EA%B8%B0%ED%98%B8

https://www.acmicpc.net/problem/1517

문제

N개의 수로 이루어진 수열 A[1], A[2], …, A[N]이 있다. 이 수열에 대해서 버블 소트를 수행할 때, Swap이 총 몇 번 발생하는지 알아내는 프로그램을 작성하시오.

(버블 소트는 서로 인접해 있는 두 수를 바꿔가며 정렬하는 방법이다. 예를 들어 수열이 3 2 1 이었다고 하자. 이 경우에는 인접해 있는 3, 2가 바뀌어야 하므로 2 3 1 이 된다. 다음으로는 3, 1이 바뀌어야 하므로 2 1 3 이 된다. 다음에는 2, 1이 바뀌어야 하므로 1 2 3 이 된다. 그러면 더 이상 바꿔야 할 경우가 없으므로 정렬이 완료된다.)

Tip & 풀이 핵심

1. '시간제한 1초' & '첫째 줄에 N(1 ≤ N ≤ 500,000)이 주어진다.'

• (시간제한이 1초이면) input 길이가 10,000이 넘어가면 O(N**2)의 알고리즘으로 절대 풀 수 없음!!!
  => Bubble sort, Insertion sort, Selection sort: O(N**2)
  => Merge sort: O(N* logN) / Quick sort
  => Counting sort

2. Merge sort에서 swap하는 과정이 있더라!

   => "어떻게 하면 Merge sort 로직에 result 구하는 코드 구현?"

모범 코드

모범 코드 보면서 효율적이고 정확하게 코드 짜는 방법을 많이 배웠다.

import sys
input = sys.stdin.readline
result = 0 #최종 결과값

N = int(input())
A = list(map(int, input().split()))
A.insert(0,0) # 0 index에 0을 추가 # index 처리 쉽게 하기 위함
tmp = [0] *(N+1) # A배열의 크기를 맞춤 # A를 바로 처리하기 부담스러우므로 복제

def merge_sort(s, e):
    global result
    if e-s < 1: return
        
    else:
        m = (e+s) // 2
        merge_sort(s, m)
        merge_sort(m+1, e)
        
        for i in range(s, e+1):
            tmp[i] = A[i]
        
        # two pointers
        k = s #현재 바꾸어야 하는 A의 index
        index1 = s
        index2 = m+1
        while index1 <= m and index2 <=e:
            if tmp[index1] > tmp[index2]:
                A[k] = tmp[index2] #swap
                result += (index2-k)
                k += 1
                index2 += 1
                # A[index2] = tmp[index1]
            
            else:
                A[k] = tmp[index1]
                k += 1
                index1 += 1
         
        while index1 <= m:
             A[k] = tmp[index1]
             k += 1
             index1 += 1
        
        while index2 <= e:
            A[k] = tmp[index2]
            k += 1
            index2 += 1
        

merge_sort(1, N) # 1번째 idx부터 N번째 idx까지 merge_sort 진행
print(result)

• global 이해 필수: https://lets-hci-la-ai-withme.tistory.com/68
• A.insert(0,0) : idx 처리 편하도록 0번째에 0value 추가
• tmp 생성: input 리스트(A) for문으로 복제 (value 값 저장하여 안전하게)
• 재귀식에서 base condition 처리, return만: if e-s<1: return
• 함수에서 return이 없을 수 있다. 단 위 경우, 전역변수인 result에 계속 값을 저장.
• 특히, Merge_sort에서 return 없이, 시작 idx(s)와 끝 idx(e)만을 입력 파라미터로 이용하여 처리 가능.
• k는 현재 처리해야 하는 A에서의 idx. 따로 지정.

내가 작성한 시간 초과 코드:

def merge_sort(inputs):
    
    if len(inputs) < 2:
        return inputs, 0
    
    else:
        mid = len(inputs)//2
        left = inputs[:mid]
        right = inputs[mid:]
        left_ , l_count  = merge_sort(left)
        right_ , r_count = merge_sort(right)
        
        merged, count = merge(left_, right_, l_count, r_count)

        return merged, count

def merge(left_, right_, l_count, r_count):
    merged = []
    count = (l_count + r_count)
    l_ptr = 0
    r_ptr = 0
    
    while l_ptr < len(left_) and r_ptr < len(right_):
        if left_[l_ptr] > right_[r_ptr]:
            # left에서 right_[r_ptr]보다 큰 원소 중 최소인 것의 idx 찾기
            s, mid, e = 0, 0, len(left_)-1

            while s <= e:
                mid = (s + e)//2
                if right_[r_ptr] == left_[mid]:
                    break
                
                elif right_[r_ptr] < left_[mid]:
                    e = mid -1
                else:
                    s = mid+1
                        
            if left_[mid] <= right_[r_ptr] < left_[e]:
                count += len(left_) - (mid+1)

            elif right_[r_ptr] < left_[s]:
                count += len(left_) - s

            elif mid > 0 and mid <= len(left_)-2:
                idx = mid+1
                while right_[r_ptr] >= left_[idx]:
                    idx += 1
                count += len(left_) - idx
            else:
                print(-1)
            
            merged.append(right_[r_ptr])
            r_ptr += 1
        else:
            merged.append(left_[l_ptr])
            l_ptr +=1
    
    while r_ptr < len(right_):
        merged.append(right_[r_ptr])
        r_ptr += 1
        
    while l_ptr < len(left_):
        merged.append(left_[l_ptr])
        l_ptr +=1
    
    return merged, count

import sys

for t in range(2):
    if t == 0:
        n = int(sys.stdin.readline())
    else:
        inputs = list(map(int, sys.stdin.readline().split()))
        print(merge_sort(inputs)[1])