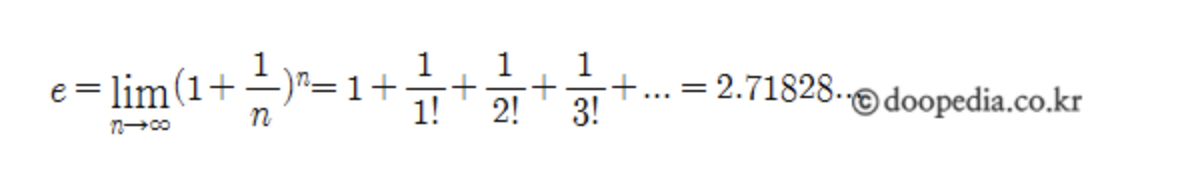
*오일러의 수 e를 통해 간단하게 연산되는 경우가 많다
(1) e를 밑으로 하는 로그를 자연로그라 한다.
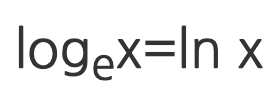
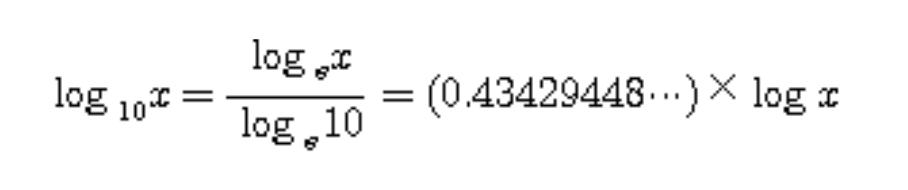
- 로그함수 ln x는 미분하면 1/x이 되어 다른 로그함수에 비해 미분 연산이 매우 간단하다.
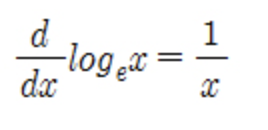
(2) e를 밑으로 하는 지수함수 e**x 또한 미분하면 자기자신 그대로인 e**x가 된다
refer to
[네이버 지식백과] 오일러의 수 [Euler's Number] (두산백과 두피디아, 두산백과)
오일러의 수 활용
Lifetime of good/bad chips → Exponential Decay
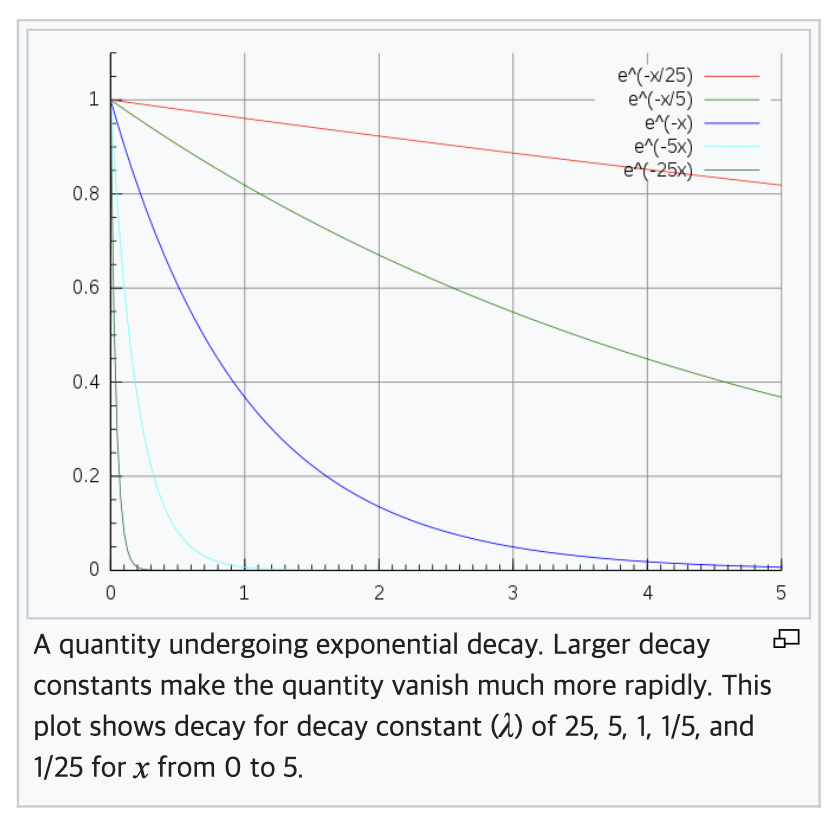
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where N is the quantity and λ (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant:
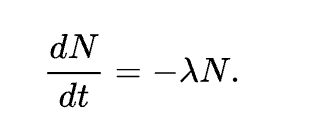
The solution to this equation (see derivation below) is:
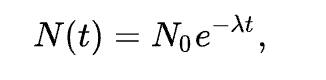
where N(t) is the quantity at time t, N0 = N(0) is the initial quantity, that is, the quantity at time t = 0.

https://en.wikipedia.org/wiki/Exponential_decay
Exponential decay - Wikipedia
From Wikipedia, the free encyclopedia Decrease in value at a rate proportional to the current value A quantity undergoing exponential decay. Larger decay constants make the quantity vanish much more rapidly. This plot shows decay for decay constant (λ) of
en.wikipedia.org
'Finance > Basic' 카테고리의 다른 글
| [FX] "금융위 "CD→KOFR 지표금리 체계 전환 본격화 시점"" 뉴스 리뷰 (1) | 2024.03.31 |
|---|---|
| [용어] 파생상품, 인수도, 마켓메이커, 베이시스, (선물/옵션) 스프레드 거래, Protective Put, Covered Call, ELS, 동적헷징, 옵션민감도 (0) | 2024.03.28 |
| [Swap] 스왑 / FX Swap, IRS, CRS (1) | 2024.03.24 |
| [FX] 용어 정리 (0) | 2024.03.21 |
| [Finance] 다양한 차익거래 & 상황/목적별 운용 방식 (0) | 2024.03.21 |