1. 채권가격정리
1) 채권가격과 채권수익률(할인율)은 역의 관계
→ 채권 매입 후 시장금리 하락 / 만기수익률 하락 / 채권수익률 하락 시 채권가격이 상승하여 매매차익을 봄
2) 만기 일정할 때, 수익률 하락으로 인한 가격 상승폭이 / 수익률 상승으로 인한 가격 하락폭보다 크다
→ 채권의 볼록성에 의함
3) 채권의 잔존기간이 길수록 '수익률 변동에 대한 - 채권가격 변동폭(듀레이션)' 크다
4) 채권가격 변동폭은 만기가 길어질수록 증가하나, 그 증가폭은 체감한다 (완만한 기울기로 증가)
*듀레이션이 길어질수록 볼록성은 체증적으로 증가함
5) 표면이자율이 낮을수록 '수익률 변동에 대한 - 채권가격 변동폭(듀레이션)'이 크다
2. 듀레이션: 채권가격의 변동성
2.1 듀레이션 개념
= (금리 변동에 따른 채권가격 변동성)
= 표면금리에 반비례, 잔존만기(이자지급기간)에 비례, 만기수익률에 반비례
= 이자지급 횟수에 반비례
2.2 듀레이션(맥컬레이 듀레이션)에 대한 두 가지 관점
1) 투자원금(P, 채권 매입가격)을 회수하는 기간: 채권의 투자원금의 가중평균 현금흐름에 대한 회수기간 (현가 기준)
= 채권의 미래 현금흐름을 회수하는 데 걸리는 가중평균 기간

ex1. 표면이율이 낮아지면 듀레이션은 길어짐
ex2. 무이표채이면 듀레이션 == 잔존만기
2) 금리 변화에 따른 채권가격의 변동성
: 금리 x% 변동 → 채권가격은 (x*듀레이션)% 변동
ex1. 이자율이 1% 하락할 경우
듀레이션이 2인 채권: 채권가격이 2% 상승
듀레이션이 3인 채권: 채권가격이 3% 상승
2.3 듀레이션 조절전략
if 수익률 하락을 예상 = 채권가격 상승을 예상
수익 극대화를 위해, 듀레이션 확대 전략을 펼침 = 수익률 하락에 따른 채권 가격 상승을 극대화함
: 표면이율(표면금리)이 낮고 잔존만기가 긴 채권을 매수
if 수익률 상승을 예상 = 채권가격 하락을 예상
손실 최소화를 위해, 듀레이션 축소 전략을 펼침 = 수익률 상승에 따른 채권 가격 하락폭을 줄임
: 표면이율이 크고 잔존만기가 짧은 채권을 매수
2.4 채권가격변동성의 특징
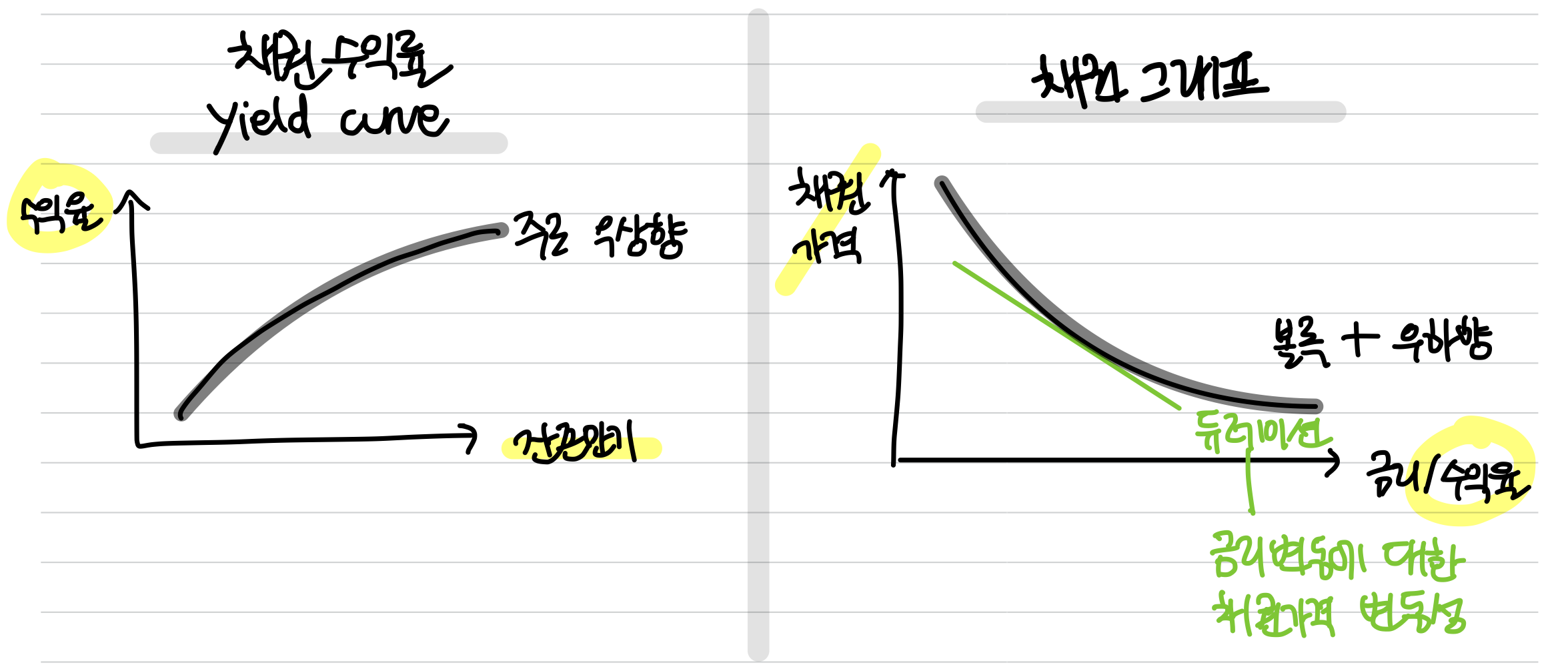
1) 채권수익율-채권가격의 반비례 그래프에서, 그래프는 아래볼록 형태를 띔
*기울기 = 듀레이션 = 금리 변화에 따른 채권가격의 변동성, 민감도
이러한 볼록성에 의해, 듀레이션 != 실제채권가격
이때 듀레이션은 그래프 특정 지점의 접선(기울기)
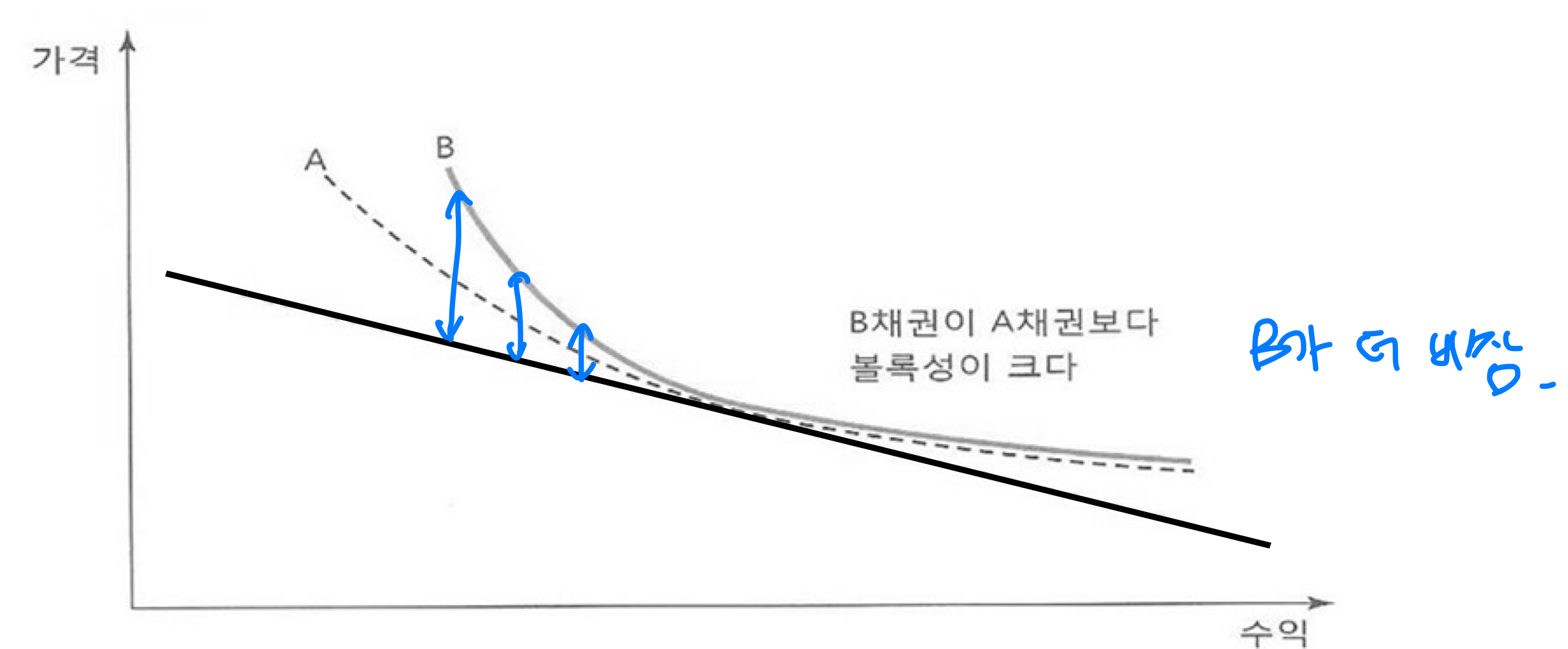
2) 금리변동폭이 클수록, (금리가 떨어졌을 때) 볼록성이 더 큰 채권의 가격이 더 올라간다
따라서, 채권은 볼록성이 클수록 좋음
투자자가는 볼록성이 더 큰 채권을 더 선호, 더 비쌈
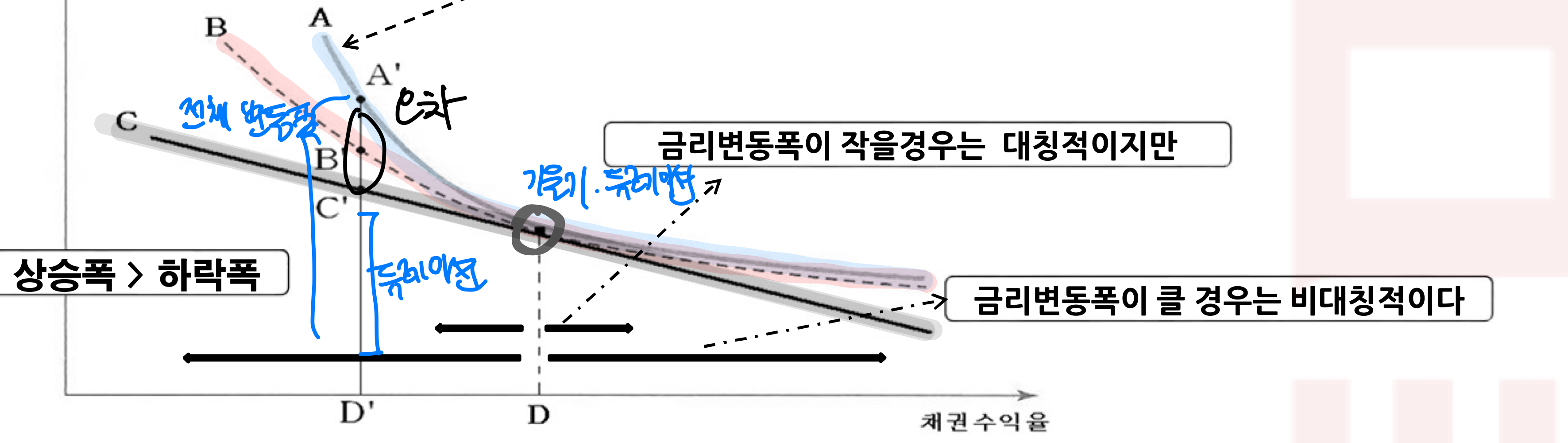
- 금리변동폭이 작을 때는, x만큼 금리가 증가/하락했을 때 채권가격의 하락/상승 폭이 대칭적임
- 금리변동폭이 클 때는, x만큼 금리가 하락했을 때 채권가격의 상승 폭이 훨씬 큼 (비대칭적)
- 채권그래프(!=yield curve)의 볼록성은 듀레이션이 증가함에 따라 가속도로 증가함
*질문: 볼록성은 클수록 좋다는데, 듀레이션은 볼록성의 여러 충분조건 중 하나일까? 아니면 과연 듀레이션도 클수록 무조건 좋은걸까? ...
3) 채권그래프 볼록성의 특징
- 채권그래프의 볼록성은 클수록 무조건 유리하다. 더 비싸다.
- 볼록성은 듀레이션 증가에 따라 체증적(가속도)으로 증가한다.
- 하나의 채권에서, 수익률이 하락할수록 볼록성은 증가한다 (이건 하나의 그래프 상에서 수익률 낮은 쪽으로 move하면 수익률 높은 쪽으로 move 할 때보다 그래프 기울기가 더 가파라진다는 것)
*채권그래프의 1차 미분 = 듀레이션
*채권그래프의 2차 미분 = 볼록성 (테일러전개에 이차미분항까지 확장한 것)
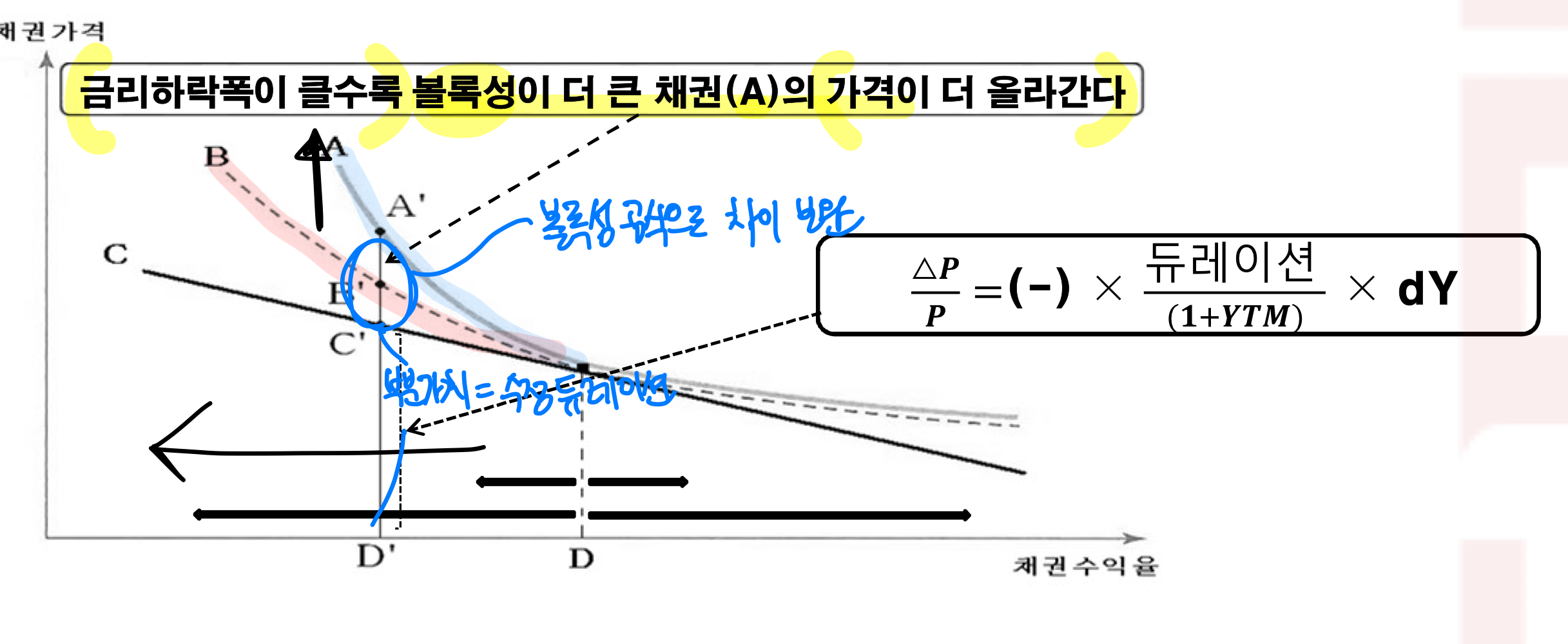
볼록성 비례공식은 듀레이션의 비례공식과 일치
볼록성 = 표면금리 반비례, 잔존만기 비례, 만기수익률 반비례
4) 듀레이션으로 측정한 채권가격 변동율
* 가격 변동율(%) != 가격 변동폭(실제 가격 단위) != 가격 변동성(성질, 맥컬레이 듀레이션으로 계산, 원금 회수기간, 가중평균)
4-1) 채권가격 변동률 (%)
= 채권가격 변동량 / 채권가격
= ( - 금리변동분) * 수정듀레이션
= ( - 금리변동분) * (맥컬레이듀레이션 / (1+만기수익률 r))
*r은 변화이전, '연후급' 명시 없으면 이자지급 한 '기'에 해당하는 것으로.
ex. 3% 금리 상승 시, (3*수정듀레이션)% 가격 상승
4-2) 채권가격 변동폭 = 변동된 가격을 실제 가격 단위로 표현 = 채권가격 변동률 * 투자원금 P
2.5 듀레이션의 용도
1. 채권가격의 민감도 (=위험으로 해석)
2. 가법성 (포트폴리오의 듀레이션: 가중평균하여 계산)
3. 헤지 비율 계산 (단순헤지, 베타헤지)
ex) 헤지는 무위험수익 추구하므로 하나는 매도, 하나는 매수.
만약 채권현물 100억(듀레이션 5)을 보유중인데, 듀레이션이 10인 채권선물(액면 1억) 매도하여 헤지하고자 하는 경우, 채권선물의 매도계약수는?
1% 금리 변화에 5% 가격 변화 * 100억만큼 (매수한 상태)
헤징하려면 매수량-매도량 비율을 일치시켜야 하고. 따라서 5*100억 = 10*1억*x개
x = 50계약
Refer to: 토마토패스 투운사 강의 자료
https://www.fidelity.co.kr/insight-and-learning/bond-investing-made-simple/bond-duration
'Finance > Basic' 카테고리의 다른 글
| [FX] 일본의 마이너스 금리 해제 (0) | 2024.03.21 |
|---|---|
| [FX] "BOJ 앞둔 통화옵션시장 움직임(24.03.19)" 뉴스리딩 (2) | 2024.03.19 |
| [macro] 거시경제 / IS-LM 모형 (4) | 2024.02.25 |
| [History] 투자은행의 간략한 역사 (0) | 2024.02.22 |
| [Issue] 홍콩의 금융위기 (0) | 2024.02.22 |