[이론] The Kalman filter, 칼만 필터

원본 출처:

(1) UoMDSS workshop

https://github.com/UOMDSS/workshops-2022-2023

 

(2) 이미지 이하 내용은 아래 글을 필요한 부분만 추출하여 정리한 것

https://blog.naver.com/PostView.naver?blogId=ycpiglet&logNo=222139077774&redirect=Dlog&widgetTypeCall=true&topReferer=https%3A%2F%2Fsearch.naver.com%2Fsearch.naver%3Fwhere%3Dnexearch%26sm%3Dtop_hty%26fbm%3D0%26ie%3Dutf8%26query%3Dkalman%2Bfilter&directAccess=false

---

 

자율주행에는, map이 필요함

센서와 데이터를 통한 맵핑(Mapping)이 필요 → 이때 필요한 작업이 바로 '확률 기반의' Localization.

*Localization: 위치 측정

*일종의 추정이론 (Estimation Theory)에 포함되는 것: 입력된 자료가 불완전하거나 불확실하더라도 사용할 수 있는 계산 결과의 근삿값 이용함. 즉, 통계적 방법과 인과관계를 기반으로 예측하는 것. 

 

자율주행차의 Localization의 경우, 필요한 데이터의 전수조사를 할 수 없기에 추정(Estimation) 기법을 동원해야 함.

모든 관측값(Measurement)는 오차(Error)를 가지고 있으며, 기술 통해 줄일 수는 있지만 완전히 없애는 건 불가능함

 

이때 칼만 필터(Kalman Filter)를 활용할 수 있다: current state를 계산할 때 control input으로 사용되는 것

- 적용 대상: GPS, 날씨 예측, 주식 예측 등.

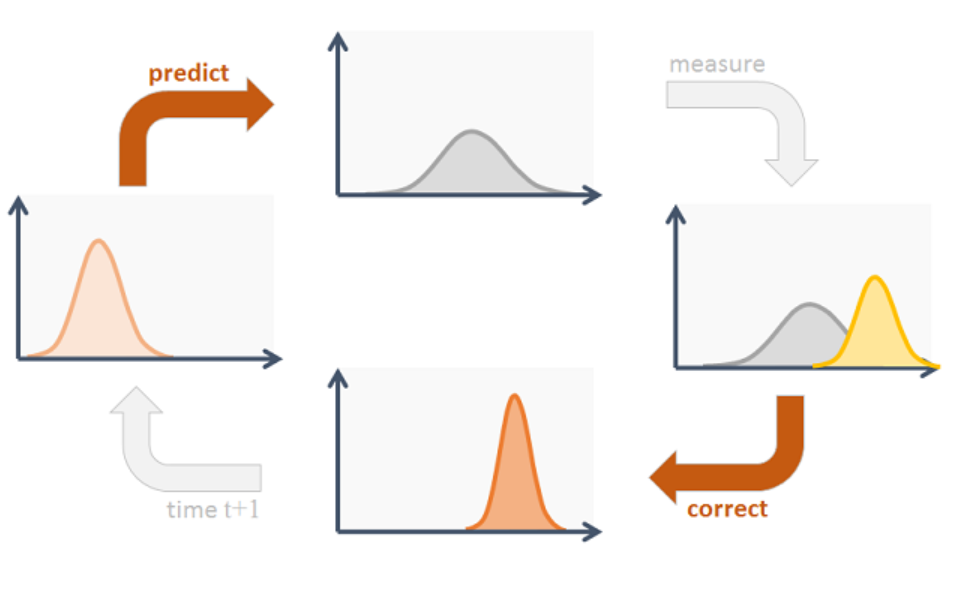
- 칼만 필터의 기본 개념: 과거와 현재의 값을 기준으로 재귀적 연산을 통하여 최적값을 추적하는 것 (상태 관측기의 최적버전)

* 필터: measured data에 포함된 noise를 필터링하는 것 → noise가 포함된 data에서 원하는 신호나 정보를 골라내는 알고리즘

                                                                                      → current state를 estimate하는 데 필요함.

- 칼만 필터는 최소제곱법(LSM)을 사용함

- 확률에 기반한 estimation이므로, 예측의 대상은 정규 분포(가우시안 분포)를 가지는 대상.

 

- 적용 상황의 2가지 조건 (1) 모션 모델과 측정 모델이 Linear (2) 정규 분포(가우시안 분포)를 따름

   물체의 measurement에 가우시안분포의 확률적 오차가 포함되고, 특정 시점의 상태가 이전 시점 상태와 선형적 관계를 가진 경우에만 적용이 가능함. 잇따른 한계 존재함.

  예측 model을 이용하여, 자율주행차의 실제 속도와 위치가 어떤 범위에 속할 것이라는 예측(Prediction)이 가능함: 칼만필터는 위치(position)와 속도(velocity) 두 변수를 랜덤 가우시안 분포로 가정함. (estimation != prediction)

 

- 칼만필터의 동작 원리:

   다음 위치를 확률적으로 predict하고,

   실제로 measure한 값을 통해 prediction과 얼마나 비슷한지 확인 후

   보정과 estimate을 한다

    => 재귀적 반복

 

- 칼만필터의 효율성: 일반적인 알고리즘은 기존 데이터를 보유해야 하므로 메모리 부담이 큼. 그러나 칼만필터는 직전 estimation과 현재에 대한 prediction만 저장하고 있으면 되는, 즉 직전값을 제외한 기존의 오래된 데이터는 버려도 되는 '재귀필터'!!

- 칼만필터의 한계: 시스템이 Linear이라는 가정 → 비선형 시스템에서 error가 커지거나 발산할 수 있음

                             noise가 가우시안 분포를 따른다는 가정 역시 어긋나는 경우가 많음.

 

- 보완책: 확장 칼만 필터(EKF, Extended Kalman Filter): most popular

              무향 칼만 필터(UKF, Unscented Kalman Filter)

              두 가지 모두 적용해보고 성능 비교하여 적용한다고 함.

              파티클 필터(Particle Filter): 추정 확률 분포를 가우시안으로 특정짓지 않는 필터 but 연산량이 많음

 

 

 

 

 

 

[수학] 칼만 필터(Kalman Filter)란 무엇인가? (로봇, 자율주행, SLAM 알고리즘)